warum konvergiert die Reihe 1/n^2 und nicht die Reihe 1/n?
Hallo
mich würde gerne interessieren warum die die Reihe 1/n^2 konvergiert und die Reihe 1/n divergiert. Man lernt das so in der Schule/in der Uni aber so wirklich hinterfragt habe ich das nie wirklich 😅
Das Monotoniekriterium für Reihen lautet:
Eine Reihe mit nichtnegativen reellen Summanden konvergiert genau dann gegen einen Grenzwert, wenn ihre Partialsummen beschränkt sind.
erreiche ich bei 1/n^2 wirklich eine Schranke und bei 1/n nicht? irgendwie kann ich mir das nur schwer vorstellen, auch wenn ich weiß das es tatsächlich so ist!
Kann mir das jemand erklären?
Danke euch
5 Antworten

Das lässt sich über das Minorantenkriterium Beweisen.
Die Reihe ist ja 1+1/2+1/3+1/4 usw.
Eine Reihe die eine Minorante ist wäre zB
1+1/2+(1/4+1/4)+usw.
Dann erkennt man, dass man hier immer 1/2 dazu addiert wodurch die Minorante eindeutig divergiert und daher auch die harmonische Reihe divergieren muss weil die ja noch schneller wächst.
Die Konvergenz von 1/n² kannst du zb über das Cauchy Verdichtungskriterium herleiten, daraus folgt dann eben eine geometrische Reihe und deren Konvergenz kann man nachweisen. Daraus kann man natürlich auch die Divergenz von 1/n ableiten.


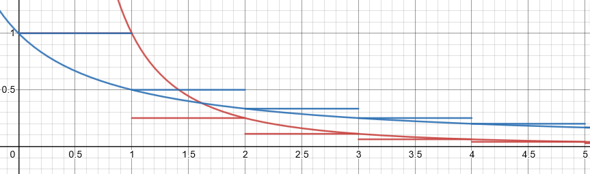
Man kann die Summen auch durch Integrale der kontinuierlichen Funktionen
abschätzen.
blau: f, rot: g
ceil ist die Aufrundungsfunktion
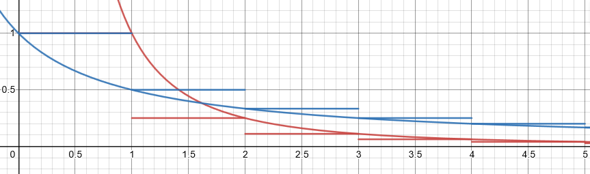
Aus der Analysis weiß manFür das Konvergenzverhalten genügt x ≥ 1.
Der Logarithmus ist unbeschränkt, aber die reziproke Funktion ist beschränkt. Man weiß also, dass die harmonische Reihe größer als was divergierendes ist, aber mit Quadrat kleiner als was konvergierendes.
Die harmonische Reihe steigt also etwa logarithmisch, bei einem Exponenten > 1 im Nenner konvergiert die Reihe.


n^2 ist immer positiv. daher ist 1/n^2 auch immer positiv, nähert sich aber beliebig nah an 0 an je grösser n wird.
n kann auch negativ sein. 1/n demnach auch und kann somit jeden Wert ausser 0 ergeben.

Die Reihe geht in diesem Fall von n=1 weg zudem steht n für eine natürliche Zahl das bedeutet n kann nicht negativ sein und 1/n kann damit auch nicht negativ sein.
Zudem konvergiert die Folge mit 1/n ja auch gegen 0 genau so wie die Folge mit 1/n². 1/n² konvergiert nur schneller.

Wir können ja einfach aus Spass die Harmonische Reihe über die Zetafunktion:
H_n = zeta(1) beschreiben.
Die Zetafunktion selbst lässt sich für Zahlen ohne Imaginärteil über die Gammafunktion beschreiben.
zeta(s) = 1/gamma(s) * integral(inf,0) (x^(s-1)/(e^(x) - 1) dx
Für die Harmonische Reihe ist s = 1.
gamma(1) = 1!, das ist logischer Weise = 1.
x^(1-1) = 1
Also bleibt:
zeta(1) = integral(inf,0) (1/(e^(x) - 1)) dx
zeta(1) = [ln(|e^(x) - 1|) - x](inf,0)
zeta(1) = ln(|1-e^-x|) (inf,0)
zeta(1) = ln(1-0) - ln(1-1)
zeta(1) = ln(1) - ln(0)
zeta(1) = 0 -(-inf)
zeta(1) = +inf
Folglich ist die harmonische Reihe divergent.
Ich hoffe das stimmt so ... Hat aber immerhin Spaß gemacht. C:


Eine kurze Suche im Netz bringt dich z.B. hier hin:
https://matheplanet.com/default3.html?call=viewtopic.php?topic=131102