Verschiedene Winkel bei Gegenvektoren?
Ich muss in einer Aufgabe den Winkel zwischen zwei Vektoren berechnen. Meine Lösung ist jedoch anders als die Musterlösung und meiner Meinung nach liegt das am Skalarprodukt, das in meinem Fall negativ ist und im Falle der Musterlösung positiv, da dort der entsprechende Gegenvektor verwendet wurde. Eigentlich kann das ja aber nicht sein, dass die Winkel unterschiedlich sind, denn die Lage der Vektoren ändert sich ja im Vergleich zum Gegenvektor nicht und somit müssten ja eigentlich auch die Winkel gleich bleiben. Werden also beim Skalarprodukt Vorzeichen einfach ignoriert oder wie sind die verschiedenen Winkel zu erklären?
3 Antworten
Ich beziehe mich auf Deinen Austausch mit Australia23.
Ja, Du hast richtig erkannt, dass Du in einem Dreieck (oder anderen Figuren) bei der Berechnung der Innenwinkel immer dafür sorgen musst, dass die betrachteten Vektoren von einem Punkt ausgehen (denn diesen Fall berechnest Du mit der Formel).
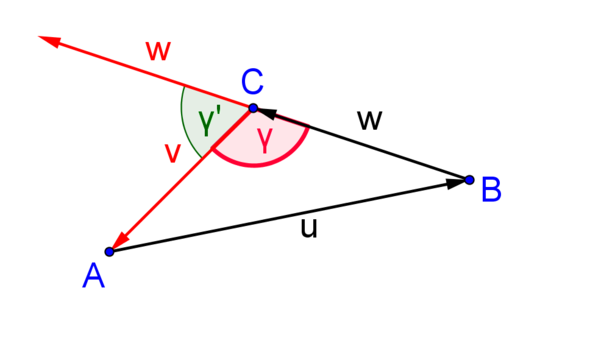
Man stellt ja bei einem Dreieck i.A. die Vektoren so auf, dass sie "im Kreis herum" laufen (vgl. meine Skizze). Wenn du also mit den Vektoren v und w arbeitest, würdest Du in diesem Fall den Außenwinkel γ' herausbekommen. Den Innenwinkel erhältst Du demnach mit dem Gegenvektor -w.
Wie Du an meinem Beispiel siehst, kann der Innenwinkel dabei durchaus größer als 90° sein.
Zur Sicherheit würde ich in einer solchen Aufgabe auch stets alle drei Winkel berechnen und dann zur Kontrolle die Summe bilden.
(Wenn Du Dir im Verfahren sicher bist, brauchst Du natürlich nur zwei Winkel mit dem Skalarprodukt zu berechnen und kannst den dritten über den Winkelsummensatz erhalten.)
Drehst du einen Vektor rum, dann hast du statt alpha den Winkel -alpha, und es ist cos(Alpha) = - cos(180-alpha), also passt alles
hab mich in meiner Antwort aber verschrieben, es soll heißen: ... hast du statt alpha den Winkel 180 - alpha
Zur Lage eines Vektors gehört auch seine Richtung. Und wenn er in die entgegengesetzte Richtung gebracht wird, wird er eben negativ (bzw. postiv, wenn er zuvor ein Minus vor sich hatte).
Das wirkt sich auf den Winkel aus.
Bei Sinusdefinition bleibt das Vorzeichen erhalten,
beim Kosinus nicht. (Das kennt man aus der Trigonometrie.)
Also darf ich für cos(alpha) nur positive werte einsetzen?
Zwei gekreuzte Vektoren erzeugen ja meist zwei verschiedene Winkel (ausser, wenn alle = 90°), welche zusammen 180° ergeben.
Kann es sein, dass z.B. nach dem kleineren Winkel gefragt ist, du aber den grösseren berechnet hast?
In diesem Fall kannst du einfach folgendes rechnen: 180° - *grösserer Winkel* = *kleinerer Winkel*
Wenn ich mich recht erinnere, kannst du um immer "direkt" auf den kleineren Winkel zu kommen, jeweils den Betrag des Skalarprodukts nehmen, also:
cos(*kleinerer Winkel*) = | a * b | / ( |a| |b| ), a & b sind Vektoren
Es handelte sich bei der Aufgabe um ein Dreieck und es waren die Innenwinkel gesucht. Das heißt, ich muss immer jeweils die Vektoren verwenden, die vom Punkt, an dem sich der Winkel befindet, "weggehen", um den kleineren Winkel zu erhalten? Also wenn Winkel Alpha am Punkt A gesucht ist, Vektor AB und AC?
Achso, aber das mit den zwei Winkeln ist klar? Also wenn du bei dem Dreieck die Vektoren über die Ecken hinaus ziehen würdest, siehst du, dass dort noch ein zweiter Winkel erzeugt wird.
* Überlegungsfehler
Also noch zur deiner Frage (hatte zu wenig Zeit es noch zu korrigieren, daher oben "*Überlegungsfehler"):
Meinen Überlegungen nach sollte das klappen, wenn du die Vektoren so wählst, bin mir aber nicht zu 100% sicher (Vektorgeometrie ist schon etwas länger her ^^).
Ich würde dir vorschlagen, es mal so zu machen, aber jeweils noch kurz zu überlegen, ob das Resultat stimmen kann (stumpfer Innenwinkel -> Winkel muss > 90°, sonst nimmst du den anderen und umgekehrt). Falls es mal nicht stimmt, hast du das Gegenteil bewiesen, also dass das nicht immer klappt (dann einfach 180°-*falscher Winkel* rechnen).
Oder jemand kommentiert hier noch, ob es sicher allgemein gültig ist ^^
ähm, nein, aber wenn du für den Vektor a den Gegenvektor -a nimmst, dann änderst du das Vorzeichen, aber durch den anderen Winkel wird das wieder geändert.