Sind krümmungsruckfreie Funktionen automatisch knickfrei?
4 Antworten
Wie stellst Du sicher, dass zwei Funktionen f und g an einer Stelle x0 krümmungsruckfrei sind? Die beiden zweiten Ableitungen müssen übereinstimmen; es muss also gelten: f´´(x0) = g´´(x0).
Ich habe mir mal zwei Funktionen ausgedacht, die an der Stelle x = 0 dieselbe zweite Ableitung besitzen. Sie haben auch denselben y-Wert (es gibt also einen Übergang von einem Graphen zum anderen). Da sie jedoch eine unterschiedliche Steigung besitzen, ist der Übergang nicht knickfrei.
f(x) = 1/2 x³ + x² g(x) = -1/2 x³ + x² + x
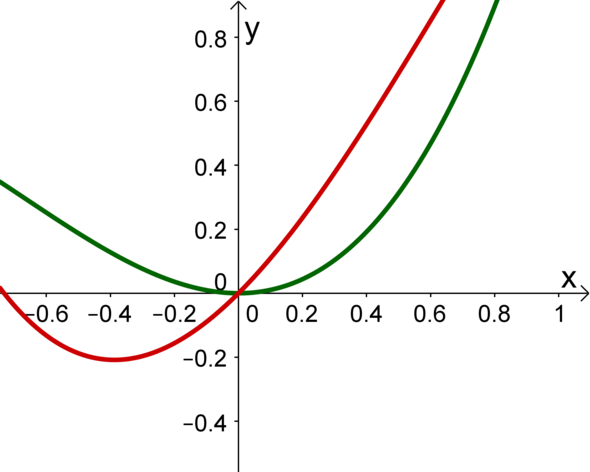
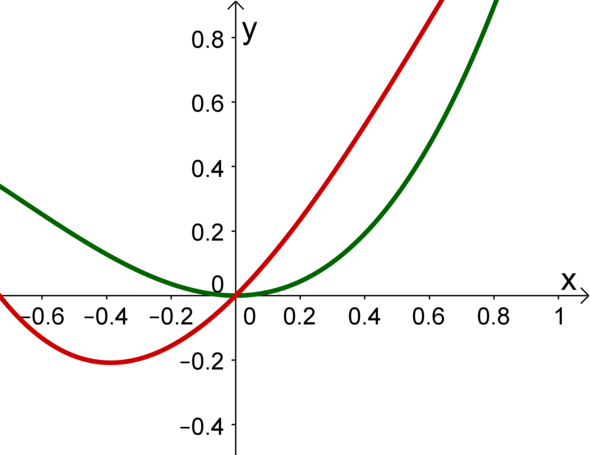
Ich habe mich bei meiner Antwort an der "üblichen" Aufgabe in der Schule orientiert, der sog. Trassierungsaufgabe. Hierbei wird i.A. ein knickfreier und krümmungsruckfreier Übergang zwischen zwei bekannten Funktionen gesucht. (Beispiel: Autobahnkreuz, bei dem ein Übergang vn der einen zur anderen Bahn geschaffen werden soll) Für jede der Übergangsstellen (das ist in meinem Beispiel x=0 gewesen) müssen dann nullte, erste und zweite Ableitung übereinstimmen.
Insofern habe ich die Frage interpretiert; gebe ich zu.
Wenn man von nur einer Funktion ausgeht, sind Deine mathematischen Argumente natürlich richtig.
nein, die freirucknickenden funktionen sind im gegensatz zu den ruckkrümmenden anders als z.b. die knickfreien krümmungen.
Ja, das sind sie!
Nur wenn sie mit Bügelfix gewaschen worden sind.
ich denke nicht, dass krümmung so einfach definiert ist.
denn das sind ja 2 funktionen, aber es geht um 1 funktion, welche krümmungsruckfrei sein soll. natürlich müsste man dann links die rote funktion und rechts die grüne funktion nehmen (oder umgekehrt), sodass die 1. ableitung nicht existiert, also auch nicht die 2. ableitung. damit ist steigung oder gar krümmung nicht definiert.
mit einer einzigen funktion wird das wohl nicht gehen. existiert die 2. ableitung, d.h. man kann überhaupt von krümmung sprechen, so ist automatisch die 1. ableitung stetig. dein f und g müssten also auch identische 1. ableitung haben! das bedeutet doch aber die knickfreiheit.