Sattelpunkt graphisch integrieren?
Servus zusammen,
ich frage mich jetzt schon seit einiger Zeit, was eigentlich beim "Aufleiten" (Integrieren) mit Sattelpunkten geschieht...
Beim Ableiten ist es logisch, dass aus einem Sattelpunkt ein Extrempunkt wird, der die x-Achse berührt (doppelte Nullstelle) und je nach positiver / negativer Steigung der Funktion eben von oben bzw. unten berührt.
Doch was wird aus einem Sattelpunkt in der Funktion f(x), wenn ich die Stammfunktion F(x) zeichnen möchte?
Ich kann es aktuell nicht nachvollziehen und bin über jede Hilfe dankbar!
Beste Grüße,
hummel
3 Antworten
Ich habe die beiden Antworten von Volens und ralphdieter gelesen.
Ich arbeite mal (in Abwandlung von Volens) mit der Funktion f(x) = x³ + 1. Dann ist eine Stammfunktion F(x) = 1/4·x^4 + x + 0,5. Zeichnung anbei.
Solche Punkte, die ralphdieter beschreibt, habe ich in meiner Schulzeit als "Flachpunkte" kennen gelernt. Diese Bezeichnung ist mir zwar seitdem nicht wieder untergekommen, beschreibt m.E. die Situation aber schön anschaulich.
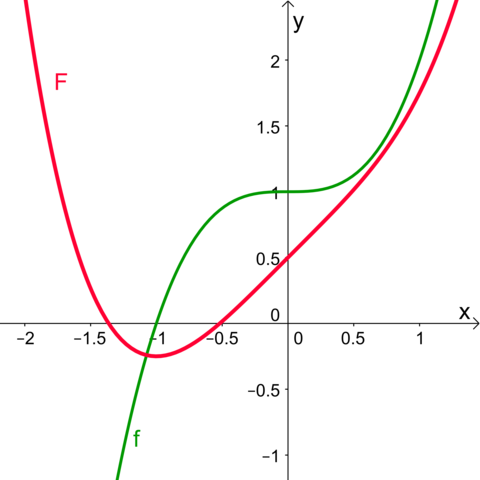
Das Bild ist super und macht es nochmal klar. Vielen lieben Dank! :-)
Die Antwort war super!
Er verschwindet in der Bedeutungslosigkeit :-)
Schon ein Hochpunkt macht sich in der Stammfunktion nur als Wendepunkt bemerkbar: davor wird sie immer steiler und danach wieder etwas weniger steil.
Ein Sattelpunkt ist nun z.B. ein "Ätsch-doch-kein-Hochpunkt". Die Stammfunktion wird also immer steiler, verläuft dann in diesem Punkt "gerade" und steigt dann doch wieder immer stärker. Sie macht also eine Linkskurve, die immer schwächer wird, bis das Lenkrad auf geradeaus steht, und kurvt dann doch wieder links weiter ("Ätsch-doch-kein-Wendepunkt"). Die Tangente schmiegt sich in diesem Punkt besonders gut an — aber das ist nichts, was wirklich ins Auge sticht.
Und ein allgemeiner Wendepunkt macht sich in der Stammfunktion nur noch bemerkbar, dass die "Krümmung" innerhalb einer Kurve hier minimal ist. Mit "Krümmung" meine ich die Änderung der Steigung (also nicht den Kurvenradius). Bei y=x² ist diese z.B. konstant. Mit bloßem Auge kann man sowas also gar nicht mehr erkennen.
Vielen Dank für die gute Antwort! :-)
Das "Ätsch-doch-kein-Wendepunkt" passt super dazu, vielen Dank!
Integriere doch einfach x³. Da hast du einen Sattelpunkt, der übrigens nicht immer auf der x-Achse liegen muss, siehe z.B. x³ + 15. Bei x³ liegt er genau im Ursprung.
Die Integration ist leicht: x⁴ / 4
Das ist eine Gleichung 4. Grades, enger als die quadratische Parabel mit dem Minimum (0|0). Das ist dort, wo bei x³ der Sattelpunkt sitzt.
Aus deinem Beispiel wird der Sattelpunkt doch dann zum Extrempunkt??
Ich dachte jetzt, dass daraus ein "Doch-kein-Wendepunkt" wird?