Potenzreihe und Ableitung berechnen?
Moin!
es geht um folgende Aufgabe bei der ich große Schwierigkeiten habe...:

Brauche unbedingt Hilfe...Danke!
2 Antworten

Bei Aufgabe 1 kannst du beispielsweise die Matrix diagonalisieren.
Man findet beispielsweise
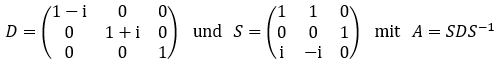
Dann kannst du
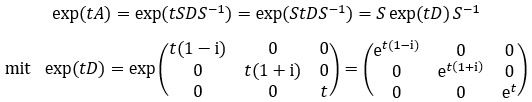
rechnen. [Grundidee: Bei Diagonalmatrizen kann man leicht die jeweilige Exponentialmatrix finden, indem man die Diagonaleinträge exponenziert.]
Das führt dann schließlich nach weiterer Rechnung zu
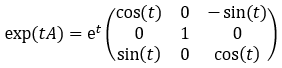
============
Bei Aufgabe 2 kann man ähnlich vorgehen. Ermittle die Jordan-Normalform und eine entsprechende Transformationsmatrix S.
Man findet beispielsweise
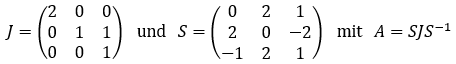
Nun kann man entsprechend in einen diagonalen Anteil und einen nilpotenten Anteil zerlegen. Bei der Diagonalmatrix kann man das Exponential leicht berechnen. Bei der nilpotenten Matrix bricht die Exponentialreihe nach wenigen Summanden ab.
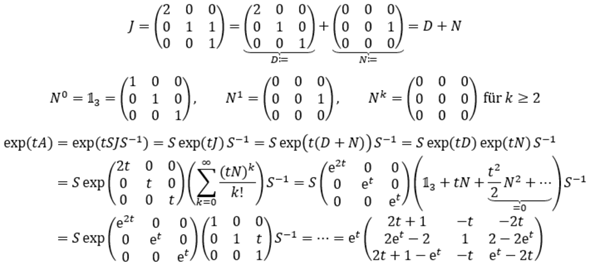
Das kannst du nun entsprechend noch nach t ableiten. Bzw. könntest du auch ausnutzen, dass nach Kettenregel
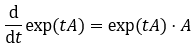
ist, wenn du das nutzen möchtest.
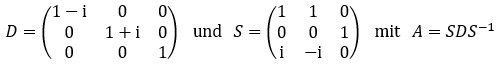
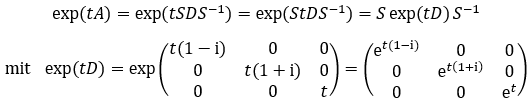
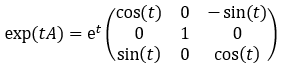
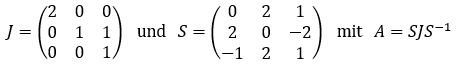
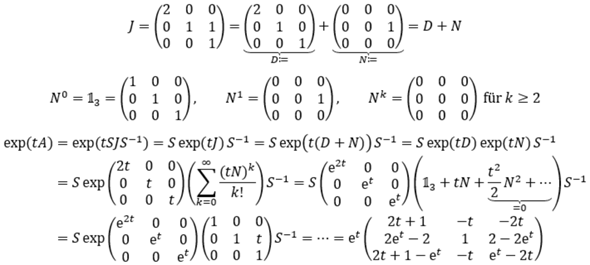
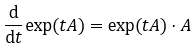


Matrizen diagonalisieren und die Exponentialfunktion auf die Diagonalelemente anwenden.
Das geht in diesen Fällen, weil die Matrizen regulär sind.
Bei nichtdiagonalisierbaren Matrizen (die sind alle singulär, aber nicht jede singuläre Matrix ist nichtdiagonalisierbar) bringt man die Matrix in eine Form, die aus zwei Teilmatrizen besteht, von denen die eine eine Diagonalmatrix ist und die andere eine nilpotente Matrix ist. Die Diagonalmatrix behandelt man wie den regulären Fall, die nilpotente Matrix hat nur endlich viele nichtverschwindende Potenzen (nach Definition von "nilpotent").

Das mit dem Diagonalisieren der Matrix bzw. das Aufsplitten in einen diagonalisierbaren und einen nilpotenten Anteil ist ein guter Vorschlag.
============
Allerdings möchte ich anmerken, dass Diagonalisierbarkeit nicht allzu viel damit zu tun hat, ob die Matrix regulär oder singulär ist.
Beispielsweise ist die Matrix
regulär, aber nicht diagonalisierbar. Daher ist beispielsweise deine Aussage
falsch.