Physik: Allgemeine Frage zu der Gleichung für Schwingungen?
Hey! Ich verstehe die Parameter in der Gleichung für Schwingungen nicht wirklich.
Die Formel lautet ja: y(t)= Amplitudesin(wot+phi0)
Die Amplitude ist klar. Die Kreisfrequenz auch. Nur was bedeutet das phi0 anschaulich? Ist das nicht die Phasenverschiebung. Aber wenn ich die Funktion in einen Plotter mal zeichnen lasse, dann ändert sich nichts wenn ich iwelche Werte für phi0 einsetze?
Danke!
4 Antworten

Du hast alles richtig erkannt. Phi ist die Phasenverschiebung gegenüber der Funktion, die durch den Punkt (0/0) geht. Phi0 verschiebt die Funktion in der X-Richtung, positve Werte nach links.
Somit wird dir jeder mathematisch Funktionsplotter eine Funktion zeichnen, die eben um phi0 verschoben ist und nicht mehr durch (0/0) geht (ausser phi0 ist 180 Grad oder Pi).
Anschaulich kann Phi0 einem Zeitpunkt entsprechen, von dem an die Betrachtung läuft, und wo eben die Schwingung nicht zufällig grad bei null war.
Ein Winkel muss es sein, weil die Sinusfunktion nur mit Winkeln (in Radiant!) als Argument umgehen kann. Kreisfrequenz mal t ist ja auch ein Winkel.
Statt phi0 kann man somit besser Omega*t0 nehmen.

Genau!
- Man kann für jede Schwingung auch den Cosinus nehmen. Das macht einfach keiner, wohl weils eine Silbe mehr zum Sprechen gibt... Erfreu dich also an cosinusförmigen Pendelbewegungen und cosinusförmiger Netzspannung.
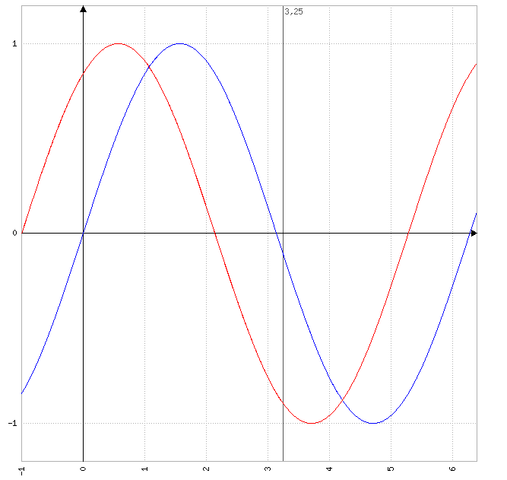
- Der Cosinusverlauf ist dem Sinusverlauf um einen Viertel der Periodendauer (2*PI/4 = 0.5Pi) voraus.
- sin(x+0.5Pi) ist also = cos(x) ; aber auch
- cos(x-0.5Pi) = sin(x) ; und somit
- sin(x+0.25Pi) = cos(x-0.25Pi)
Kannst du mit jedem beliebigen Wert auf dem Taschenrechner testen (Modus "rad" natürlich).

Die harmonische Schwingung y = f(t) = y(max) · sin (ω·t + φₒ) besitzt den Nullphasenwinkel φₒ. Das bedeutet, dass diese Funktion zum Zeitpunkt t = 0s die Elongation y = f(t) = sin(φₒ) besitzt. Der Graph der Funktion der
harmonischen Schwingung y = f(t) = y(max) · sin (ω·t + φₒ) ist dadurch im Vergleich zum Graph der Funktion y = f(t) = y(max) · sin (ω·t) um den Nullphasenwinkel auf der Abszisse in negativer Richtung, also nach links verschoben.
LG

Da phi wenn ich mich recht erinnere einen Winkel darstellt, gehe ich davon aus wir reden von der mathematischen Schwingung, also vom Federpendel, und nicht vom Federpendel. Phi stellt den winkel da, den das pendel aus der position y=0 aus betrachtet einnimmt. Wenn ich mich richtig erinnere :) Zudem ist mir unbekannt das Phi an der stelle eingesetzt wird O.o Wir haben phi immer als y genommen wenn wir bei der mathematischen Schwingung waren, die Fomel lautete Phi(t)=A sin (wt)*B cos (wt) Kp was das für ne Formel ist die du da hast :D

φ₀ ist im Allgemeinen etwas, was sich aus den Anfangsbedingungen ergibt. Anschaulich ist es die Auslenkung zum Zeitpunkt t = 0 (angenommen du nimmst den Sinus).
Wenn du φ₀ im Funktionenplotter änderst, siehst du, wie sich der Ganze Graph nach links oder rechts verschiebt und daher zum Zeitpunkt t = 0 verschiedene Werte auftreten.
Danke! Man kann ja den sinus oder den cosinus wählen. Wenn ich jetzt den sinus wähle und für phi0 +0,5pi einsetze...habe ich dann die gleiche Funktion? Oder muss ich -0,5pi einsetzen?