[Mathe] Ableiten - sind meine Aufgaben richtig?
Guten Tag,
kann jemand mal schnell darüber schauen (stichprobenartig), ob ich die Funktionen richtig abgeleitet habe? :-) Sind die ersten Übungsaufgaben, die ich nach der Einführung in das neue Thema gerechnet habe.
Nicht, dass ich mir noch etwas falsch gerechnetes verinnerliche. 💪
Vielen Dank für deine Hilfe. 💚


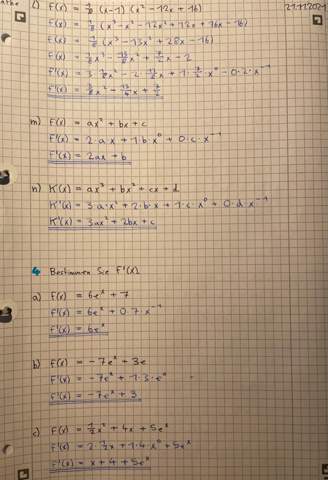

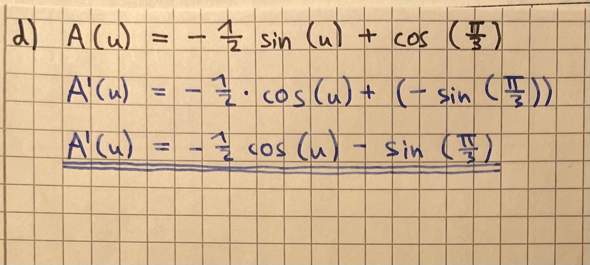
1 Antwort
Bei 3 j.) ist aus - 4 * u auf einmal - 1 geworden, da solltest du noch mal drüber schauen.
Bei 4 b.) ist aus 3 * e auf einmal abgeleitet 3 geworden, obwohl in 3 * e gar kein x drin ist.
Bei 5 d.) ist aus cos(pi / 3) auf einmal abgeleitet - sin(pi / 3) geworden, obwohl da gar kein u drin ist.
Weitere Fehler sind mir nicht aufgefallen, aber ich habe nur ganz schnell drüber geschaut, kann sein, dass ich was übersehen habe, aber 3 j.) und 4 b.) und 5 d.) solltest du noch mal anschauen.
Kannst du mir die Aufgabe 5 d) noch einmal genauer erklären?
Beim ableiten wird ja immer
sin(x) zu cos(x)
cos(x) zu -sin(x)
-sin(x) zu -cos(x)
-cos(x) zu sin(x)
Das ist mir bekannt.
Aber einmal ist hier das x drin und einmal nicht, muss man dann trotz dieser Ableitungsregel folgendes rechnen:
cos(pi/3)
0 * cos(pi/3) * x^(-1)
Ja, und 0 * Irgendwas = 0
Deshalb fällt cos(pi / 3) beim Ableiten komplett weg.
Du kannst dir merken --> Terme, in denen die Variable, nach der abgeleitet wird, nicht vorkommt, werden wie eine Zahl behandelt, sie fallen also beim Ableiten weg.
Dann habe ich Aufgabe 4 f) auch falsch 😬 Danke für deine Hilfe 😊
Stimmt, du hast recht, 4 f.) ist leider auch falsch. Aber das hast du ja jetzt zum Glück erkannt ;-))
Ich bin froh, dass es Leute wie dich gibt, sonst hätte ich im Mathe nicht immer eine 1 💪 🙏
Das hast du schon dir selbst zu verdanken. Du hast fleißig Aufgaben trainiert und hast erkannt, dass es gut ist nachzufragen um die eigenen Ergebnisse zu überprüfen.
Ich habe noch eine Frage zu einer anderen Aufgabe:
„f(x) = sin (pi/6) * e^(x) + e^(3) * x^(2)“
Ich habe folgendes berechnet:
f‘(x) = e^(x) * sin(pi/6) + 2 * e^(3) * x
f‘(x) = e^(x) sin(pi/6) + 2e^(3) x
Ist das richtig? Und wo schreibe ich das hoch 2 in der letzten Rechenzeile hier hin? Darüber wird ja gerechnet „2 * e^(3) * x“ steht das hoch 3 dann nur hinter dem 2e oder hinter allem (2ex^(2))?
Wie kann man sich das merken, wie man das schreibt?
Erstmal, dein Ergebnis ist vollkommen richtig.
Das einzige, wo ich ein ^ 2 sehe ist bei (e ^ 3) * x ^ 2 und die Hochzahl ist ja in der nächsten Zeile als der Faktor 2 vor dem (e ^ 3) gelandet, die Hochzahl von x ^ 2 hat sich um 1 reduziert, also von x ^ 2 zu x ^ 1 was man als x schreiben kann, was du auch getan hast. Ist es das was du wissen wolltest ?
Nein, sondern wenn man von dieser Spalte weitergeht
„f‘(x) = e^(x) * sin(pi/6) + 2 * e^(3) * 3“
Wohin hier am Ende das ^(3) kommt. Also man rechnet ja am Ende „2 * e^(3) * x“ und ich weiß nicht ob man es so schreibt:
„f‘(x) = e^(x) sin(pi/6) + 2e^(3) x“
ODER so:
“f‘(x) = e^(x) sin (pi/6) + 2ex^(3)
Das ^ 3 kommt daher, weil e^(3) in der Originalfunktion steht. Da e ^ (3) ja nichts anderes als eine Zahl ist oder der Stellvertreter für eine Zahl ist wird das wegen der Konstantenregel vollkommen unverändert übernommen, das 2 * davor kommt von x ^ 2, was von x ^ 2 zu x wird.
f‘(x) = e^(x) sin(pi/6) + 2e^(3) x“ ist richtig. x ^ 2 kann ja auch beim Ableiten von x ^ 2 nicht plötzlich zu x ^ 3 werden.
Ja das habe ich verstanden :D
Aber ich weiß nicht wie man das am Ende dann schreibt, also hier die Spalte bevor es als Ergebnis steht:
„f‘(x) = e^(x) * sin(pi/6) + 2 * e^(3) * 3“
Ergebnis Möglichkeit 1:
„f‘(x) = e^(x) sin(pi/6) + 2e^(3) x“
ODER
Ergebnis Möglichkeit 2:
“f‘(x) = e^(x) sin (pi/6) + 2ex^(3)
.
f(x) = sin (pi / 6) * (e ^ x) + (e ^ 3) * x ^ 2
f´(x) = sin (pi / 6) * (e ^ x) + 2 * (e ^ 3) * x
reicht das als Erklärung ?
Wie du sehen kannst bleibt (e ^ 3) als Faktor vollkommen unverändert erhalten, nur x ^ 2 hat sich verändert, indem x ^ 2 zu x wurde und der Faktor 2, der aus dem ^ 2 stammt, vor dem ganzen Term noch davor geschrieben wurde.
Genau aber dann steht es so da (Steht in der Lösung dann so wie du geschrieben hast ist Möglichkeit 1):
Möglichkeit 1:
2 * e^(3) * x (so hast du es auch geschrieben)
Möglichkeit 2:
2ex^(3)
(so hast du es nicht geschrieben, so wäre es falsch, oder?)
Ja, so wäre es falsch !, weil es dann so verstanden werden muss. dass 3 die Potenz von x wäre, also dass x hoch 3 da stehen würde, was ja falsch ist.
Hammer, danke dir für deine schnelle Hilfe 💪💯💚