Inwiefern hängen Ableitungsfunktion und Sekantensteigungsfunktion zusammen?
Die Frage sagt es ja schon. Also wie hängen diese beiden Funktionen zusammen und warum. Ich weiß, dass die Graphen der Ableitungsfunktion und der Sekantensteigungsfunktion, wenn man von der gleichen Funktion ausgeht, liegen übereinander, aber wieso?
2 Antworten
Gegeben sei eine differenzierbare Funktion f(x). Wenn du die Steigung einer Sekante durch die Punkte P1=(x,f(x)) und P2=(x+Δx, f(x+Δx)) nimmst und dann das Δ gegen 0 streben lässt erhälst du die Tangente durch den Punkt P1 und somit die Steigung im Punkt P1, also die Ableitung von f(x) im Punkt P1.
(Siehe auch Bild, mein Δx ist im Bild ein h.)
Falls noch was unklar ist, kannst du gerne nachfragen :)
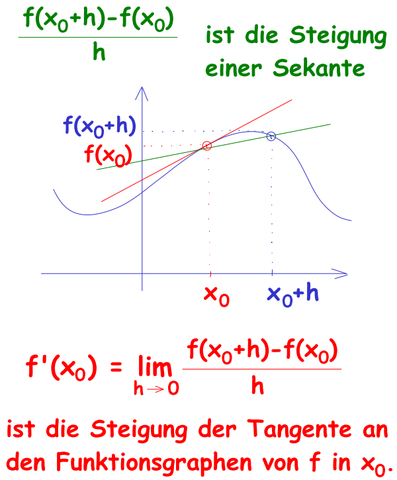
Die Ableitung g einer Funktion f gibt die Steigung einer Tangente t im Punkt f(x1) an.
Eine Tangente ist eine Extremform einer Sekante, bei der beide Punkte auseinanderliegen (Sekante geht ja durch 2 Punkte)
Dementsprechend wäre eine Sekante "im" Punkt f(x) eine Tangente deren Steigung wiederum in der Ableitung g gegeben ist