Herz berechnen?
Ich muss den Umfang und Flächeninhalt von diesem herz berechen, da ich jedoch kein wirkliches Ergebnis erhalte, wollte ich fragen ob es jemand brechen kann? Ps eine gitterkonstante=a
4 Antworten

Da man in Kommentaren keine Bilder anhängen kann, neue Antwort.
Annahme: 1 Einheit = 1 cm
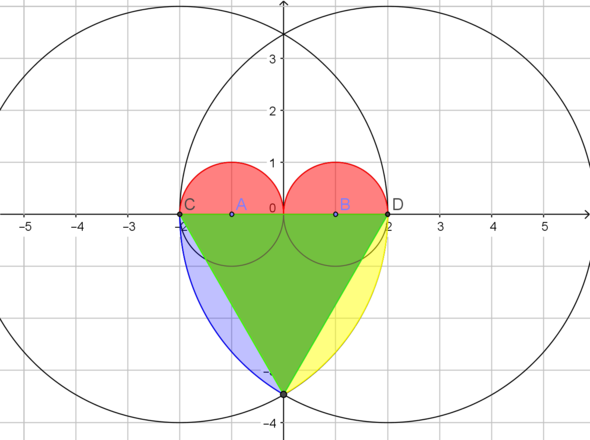
Das Herz besteht aus 2 Halbkreisen mit Radius 1 cm (rot), sowie zwei Sechstelkreisen (gelb und blau) mit Radius 4 cm. Davon musst du das gleichseitige Dreieck (grün) abziehen.
Gesamtfläche also pi + 2 * 1/6 * 16 pi - 4 * wurzel(3) = 12,97 cm²
Der Umfang ist 2 pi + 2 * 1/6 * 2 * pi * 4 = 14/3 pi = 14,66 cm
Schöne Aufgabe :-)

Vorab:
Dadurch dass die Spitz des Herzens unten nicht auf einem Knotenpunkt liegt, macht es das schon mal schwierig.
Du müsstest auf jedem Fall mal ablesen mit Lineal oder Co., wo groß der Abstand zum nächsten Knotenpunkt dort ist.
Prinzipiell musst du das Teil mal in einige grundlegende geometrische Körper zerlegen:
Die beiden Teile oben sind Halbkreise mit Radius a. Deren Flächeninhalt zu berechnen dürfte nicht schwer werden.
Eher schwierig ist die Frage, welche geometrische Form die beiden unteren teile haben.
Sind das Teile eines Kreises, (mit ziemlich großem Radius), deren Mittelpunkt weit weg vom Mittelpunkt der Figur liegt?
Wichtige Frage zu dem Thema:
Wie hast du denn die beiden unteren Teile gezeichnet?
Von Hand sicher nicht, dafür ist es zu schön.
Mit Zirkel?
Welchen Radius hast du eingestellt und wo hast du eingestochen (=Mittelpunkt)?
Denn mit den Infos ließe sich die Aufgabe weiter bearbeiten.
Man könnte wohl auch mit Zirkel die beiden Mittelpunkte der beiden Keissektoren zeichnerisch konstruieren.
Ich mach jetzt mal Folgendes:
Ich führ ein koordinatensystem ein (macht das Ganze viel anschaulicher):
Ganz oben links in der Ecke ist der Koordinatenursprung (der Punkt (0,0) sozusagen).
Und nach rechts geht die positive x-Achse, nach unten die positive y-Achse.
Dann sind die beiden oberen Teile Halbkreise um die Mittelpunkte
(1,1) und (3,1).
Übrigens: wenn ich hier (1,1) schreibe, ist damit 1 gitterkonstante nach rechts und eine nach unten gemeint)
Dann vermute ich weiter:
Der teilkreis unten rechts ist eigentlich ein nich ganz vollständiger Viertelkreis mit Radius 4 um den Punkt (0,1).
Das gleiche spiegelverkehrt für den linken Kreisteil mit Radius 4a um (4,1).
Wie man nun aber jeweils den Teil des Kreissektors innerhalb des Herzens berechnet, bin ich gerade etwas überfragt.
Aber zumindest haben wir das ganze Mal in seine Bestandteile zerlegt:
2 vollständige kleine halbkreise mit Radius 1a
und 2 mal ein Teil eines Viertelkreises mit Radius 4a.
Ersteres ist direkt berechenbar, bei Letzterem braucht man sicher den einen oder anderen Trick.
Hier mal ein Bild:
http://www.directupload.net/file/d/4501/g8gpha32_png.htm
Die Umrandung zeigt die zugrunde liegende Figur, der Bereich dessen der farblich gekennzeichnet ist, muss berechnet werden.
Mittlerweile habe ich auch schon eine Idee:
Siehst du die lila Linien?
Die lila Linie unten rechts zusammen mit der waagrechten roten Linie oben bildet einen Kreissektor, der unter Anderem den kompletten roten Bereich umfasst.
Wenn du von diesem das rechte lila Dreieck abziehst , erhälst du haargenau den kompletten roten bereich.
1.Zuerst musst also erst mal den Winkel oben rechts (w im Bild) mit Geodreieck oder so messen (könnte man auch berechnen aber das würde es nur noch komplizierter machen).
2.Damit und mit einer Formel aus dem internet für den Flächeininhalt eines Kreissektors mit Winkel (eben gemessen) und Radius=4a kriegst du den Flächeninhalt des Kreissektors.
3. Für das rechte lila Dreieck berechnest du bzw. guckst die Formel nach für den Flächeninhalt eines rechtwinkligen Dreiecks wenn 1 Seite mit Länge 2 a und der daran anliegende Winkel w bekannt sind.
4. Du ziehst vom Flächeninhalt aus 2. den Flächeninhalt von 3. ab.
5. Voila! Du kennst den Flächeninhalt der roten Fläche.
Nun wiederholst du das theoretisch für den grünen bereich spiegelverkehrt.
Praktisch ist das ganze symmetrisch, spiegelverkehrt und Co. und du kannst direkt schließen dass der Fächeninhal des grünen gleich groß dem des roten Bereichs sein muss.
Joa, insofern du anfangs den Flächeninhalt für den blauen und gelben Halbkreis berechnet hast, musst du das Alles nur noch zusammen zählen und erhälst den Flächeninhalt des gesamten herzens.
Ich weiß, dass war wahrscheinlich wesentlich umständlicher geschrieben als nötig.
Frag einfach nochmal wenn du was nicht verstehst oder etwas unklar ist. :-)

Ergänzend zu densch92:
Nix messen ! Der Winkel w ist 60° denn cos(60°) =1/2.
Damit ist ein Kreissektor ein sechstel des Vollkreises. Einmal mit Mittelpunkt oben links und einmal oben rechts. Davon das gleichseitige Dreieck abziehen, das die Schnittfläche der beiden Sektoren darstellt.

In der Figur, die du noch nachgeliefert hast, kann man erkennen, dass das Herz von zwei Halbkreisen und von zwei Kreisbögen begrenzt wird. Die entsprechenden Kreismittelpunkte sind etwas fetter markiert und haben jeweils "schöne" ganzzahlige Koordinaten. Die Flächen der beiden Halbkreise (oben) sind ganz leicht zu ermitteln. Für den Rest musst du mit Sektorflächen und Dreiecksflächen umgehen. Tipp: berechne zuerst mal den Zentriwinkiel der beiden Kreisbögen bzw. Sektoren !