Geraden und Ebenen in Körpern Aufgabe kann mir wer helfen?
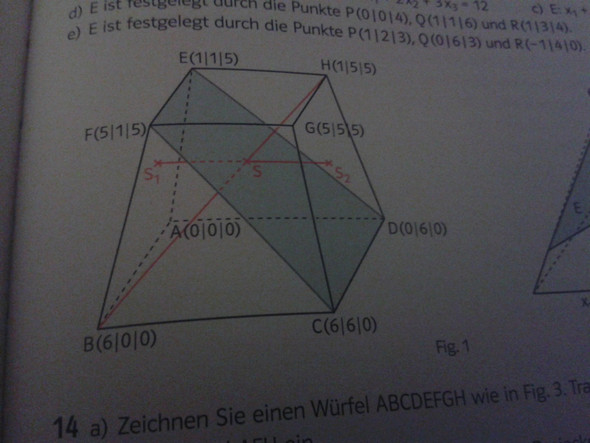
Die Abbild zeigt einen Pyramidenstumpf mit quadratischer Grundfläche. a) Die Gerade durch die Punkte B und H schneidet das Trapez im Punkt CDEF im Punkt S. Berechnen Sie die Koordinaten von S b) Die Punkte F und G legen eine Gerade fest. Die Parallele dieser Geraden durch den Punkt S schneidet die Trapeze ABFE und CDHG in den Punkten S1 und S2. Berechnen Sie deren Koordinaten
1 Antwort

Hallo,
aus den gegebenen Punkten kannst Du eine Punkt-Richtungs-Form der Geraden und der Ebene aufstellen, in der das Trapez liegt und beide gleichsetzen.
Ein Punkt, der auf jeden Fall auf der Geraden liegt, ist (6/0/0).
Den Richtungsvektor bekommst Du, wenn Du Punkt B von Punkt H abziehst, also:
(1/5/5)-(6/0/0)=(-5/5/5).
Die Geradengleichung lautet also (6/0/0)+l*(-5/5/5).
Die Ebenengleichung bekommst Du genauso, nur daß Du hier zwei linear unabhängige Richtungsvektoren benötigst.
Du kannst Punkt C (6/6/0) als Aufpunkt und D-C und F-C als Richtungsvektoren nehmen und bekommst als Gleichung für die Ebene:
(6/6/0)+m*(-6/0/0)+n*(-1/-5/5).
Das setzt Du nun gleich und erhältst drei Gleichungen:
6-5l=6-6m-n
5l=6 -5n
5l= 5n
Aus Gleichung 3 kannst Du sofort ablesen, daß l=n ist, so daß Du die zweite Gleichung so schreiben kannst:
5l=6-5l, also 10l=6 oder l=3/5 und n=3/5.
Setzt Du dies in die erste Gleichung ein, bekommst Du:
6-3=6-6m-3/5
6m=12/5
m=2/5
Nun kannst Du entweder l in die Geradengleichung einsetzen oder m und n in die Ebenengleichung (die Geradengleichung ist einfacher zu8 berechnen, also l=3/5):
(6/0/0)+(3/5)*(-5/5/5)=(3/3/3), die Koordinaten für S.
Herzliche Grüße,
Willy