Funktion mit komplexen Definitionsbereich: Globales Extrema bestimmen?
Kann mir jemand den Rechenweg und die Lösungen zu 7.10 (b) sagen.

Ich habe als Minimum –8 und als Maximum 8 raus
(an den Stellen 2i und –2i).
Ist das korrekt?
Wenn ich die Funktionsgleichung umschreibe, komme ich auf
f(z) = 3 Re(z) – 4 Im(z).
Der größtmögliche Wert ist doch dann, wenn der Teil mit dem betraglich größten Vorfaktor (hier –4) den größt/kleinst möglichen Wert bekommt.
Mit der Bedinung |z| ≤ 2 ist das doch für z = 2i und z = –2i der Fall, oder?
Ich sehe schon bei Wolfram|Alpha, dass es falsch ist, aber ich weiß nicht warum...
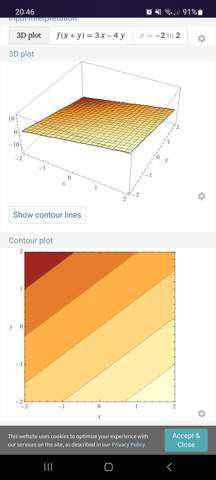
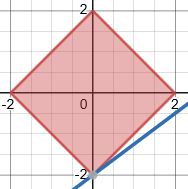
Wenn man in def unteren Grafik jetzt einen Kreis mit dem Radius Zwei um den Ursprung zeichnet (also die Definitionsmenge), sieht man schnell, dass das
Maximum bei √2(1–i) und das
Minimum bei √2(i–1) angenommen wird.
Wie kommt man darauf?
Das oben ist falsch.
Ich checke gerade nichts mehr...
3 Antworten

Der größtmögliche Wert ist doch dann, wenn der Teil mit dem betraglich größten Vorfaktor (hier –4) den größt/kleinst möglichen Wert bekommt.
Eben nicht.
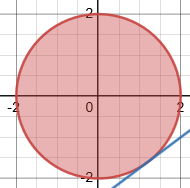
Punkte mit demselben Zielfunktionswert c ∈ ℝ liegen jeweils auf der Gerade f(z) = c. Je weiter man die Gerade parallel nach rechts unten verschiebt, desto größer wird der Zielfunktionswert. Zulässige Punkte liegen im geschlossenen Kreis |z| ≤ 2. Man muss die Gerade also so weit verschieben, dass sie den Kreis gerade noch berührt.
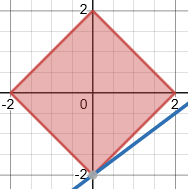
Deine Vorgehensweise wäre richtig, wenn es sich nicht um den komplexen Betrag bzw die euklidische Norm handeln würde, sondern um die Betragssummennorm, in dem Fall also die Nebenbedingung |Re(z)| + |Im(z)| ≤ 2 wäre:
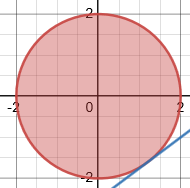
Da die Zielfunktion linear ist, werden sowohl Minimum als auch Maximum am Rand angenommen. Durch Umwandeln der Nebenbedingung |z| ≤ 2 in |z| = 2 kann das Optimierungsproblem gelöst werden.
Nun zur Lösung des Problems
Ich betrachte das als Extremwertproblem über ℝ² und schreibe z als x + iy.unter der Nebenbedingung Das Lösungsverfahren wird bereits in der Schule behandelt.
- Auflösen der Nebenbedingung nach einer Variable
- Einsetzen in die Funktion, sodass sie nur noch von einer Unbekannten abhängt
- Ableiten und Nullsetzen
- Auflösen
- Jetzt müsste man noch in y(x) einsetzen um y zu bekommen und überprüfen für welche der möglichen Werte für x und y ein Hochpunkt bzw Tiefpunkt vorliegt.
Alternativ gäbe es für die Lösung von mehrdimensionalen Extremwertproblemen noch das Verfahren der Lagrange-Multiplikatoren.

Die Antworten passen irgendwie nicht zu meiner Frage. Vielleicht habe ich mich falsch ausgedrückt.
Ich suche die Extrema von f mit der Definitionsmenge M und
f(z) = 3 Re(z)–4 Im(z).
Die Koordinate muss also drei Komponenten haben (Re(z)|Im(z)|f(z)).

Ja, das ist die Definitionsmenge. Und der Berührpunkt mit der Gerade ist der Punkt (Re(z), Im(z)), für den f(z) maximal wird. Um den Funktionswert zu bekommen, muss man z in f einsetzen.

Aber wie kommst du auf die Geradengleichung?


Den Lösungsweg kann ich nachvollziehen, aber im Buch (woher ich die Aufgabe habe) kam noch keine Defferentialrechnung vor.

Man könnte sich auch überlegen, dass es sich bei \tilde{f} um ein Skalarprodukt handelt und das wird bei gleichen Beträgen am größten, wenn die Vektoren in die gleiche Richtung zeigen.
Vielleicht wird trotzdem etwas Schulmathematik angenommen, auch wenn das nicht explizit erwähnt wird. Wenn es sich um ein Buch über Funktionentheorie handelt, geht es in dem Kapitel über Differentialrechnung wahrscheinlich um komplexe Differenzierung und reelle könnte vorausgesetzt sein.

Nene, im Buch wird nur das Wissen aus den vorherigen Kapiteln angenommen (sonst wäre es die erste Aufgabe, bei der es nicht so ist). Das ist ein Lehrbuch, dass auch ganz von vorn beginnt.

Auf Seite 230 ist ein Beispiel vorgerechnet. Das könnte man analog machen, mit dem ganzen Quadrieren:
Re[(3+4i)] ≤ |(3+4i)z| = |3+4i| |z| = 5 |z| ≤ 5 ⋅ 2 = 10
Jetzt wird angenommen, das so ein z mit f(z) = 10 tatsächlich existiert.
Re[(3+4i)(x+iy)] = 3x - 4y = 10
⇒ 9x² - 24xy + 16y² = 100
⇔ - 24xy = 100 - 9x² - 16y²
⇒ 576x²y² = (100 - 9x² - 16y²)²
⇔576x²(4 - x²) = (100 - 9x² - 16(4 - x²))²
⇔ 2304x² - 576x⁴ = (36 + 7x²)²
⇔ 2304x² - 576x⁴ = 49x⁴ + 504x² + 1296
⇔ 625x⁴ - 1800x² + 1296 = 0
⇔ (25x² - 36)² = 0
⇔ 25x² - 36 = 0
⇔ (5x + 6)(5x - 6) = 0
⇔ x = ± 6/5

Oh...
Das f(z) kleiner gleich 10 ist, habe ich auch genau so herausgefunden.
Ich dachte nur, dass das Gleichsetzen von f(z) und 10 nicht das sein sollte, was man machen sollte (weil so viel Rechnerei). Aber gut.
Vielen Dank dir! :D

Also du willst im Grunde die Funktion f(a,b) = 3a-4b auf der Kreisscheibe minimieren/maximieren.
Betrachten wir dazu zuerst die Niveaulinien, das sind die Linien, wo die Funktion Konstant sind. Setzte dazu c aus R fest.
Die Gleichung 3a-4b=c wird dann von den Punkten
((c+4b)/3, b) mit b aus R gelöst.
Das entspricht den Geraden Im R^2 mit Aufpunkt c/3 und Richtungsvektor (4/3, 1).
Bestimmen wir nun einen Orthogonale Vektor zum Richtungsvektor.
Das ist hier einfach nur (-1, 4/3), bzw zur Einfachheit (-3, 4)
Wir wissen, dass die Funktion den Wert nicht verändert, wenn man in der Richtung (4, 3) geht, es ist nur entscheidend wie weit man in der Richtung (-3, 4) geht. Und es sollte auch klar sein, dass die Funktion entlang dieser Ursprungsgerade streng monoton ist)
Somit erhälst du die Extrema, wenn du dich am weitesten in der Richtung (-3, 4) vom Ursprung entfernst. Die Punkte erhälst du, wenn du den Vektor normierst und dann mit ±2 multiplizierst.

Nach dem Maximumprinzip sind Minimum und Maximum auf dem Rand zu suchen, es geht also um die Maxi-/Minimierung von f(a+ib) = 3a-4b auf a^2 +b^2 = 4.
Maximum bei (6/5, -8/5)
Minimum bei (-6/5, 8/5)
-----
Edit: Maximumprinzip (der Funktionentheorie) ist nicht anwendbar, Lösung stimmt trotzdem ....

Maximum bei (6/5, -8/5)
Minimum bei (-6/5, 8/5)
Aber wenn z=6/5 ist, dann ist f(z)=18/5=3.6
Aber alleine f(2i)=8 ist schon größer als als f(6/5).
Die Antworten passen irgendwie nicht zu meiner Frage. Vielleicht habe ich mich falsch ausgedrückt.
Ich suche die Extrema von f mit der Definitionsmenge M und
f(z) = 3 Re(z)–4 Im(z).
Die Koordinate muss also drei Komponenten haben (Re(z)|Im(z)|f(z)).

Mit (6/5, -8/5) ist gemeint a= 6/5, b= -8/5 (Koordinatenschreibweise (a,b) für z=a+ib), die Berechnung des Maximums wollte ich dir überlassen, es ist 10.


Ich verstehe aber nicht, wie du auf dieses Paar gekommen bist... :(

Man kann a = (4- b^2)^(1/2) in 3a-4b einsetzen, macht 3(4- b^2)^(1/2)-4b. Das nun ableiten, Null setzen, gibt b=-8/5, damit a= 6/5

Dein Kreis ist also nur die Definitionsmenge von f.