Bernoulli-Binomialverteilung Mindestens ausrechnen?
Hallo, ich schreibe bald mein Abitur und komme bei folgender Aufgabe nicht weiter ?
Bei einem Interview werden 20 Schüler befragt ob sie ein Handy besitzen.
a) Berechne die Wahrscheinlichkeit das keiner der Schüler ein Handy hat.
b) Berechne die Wahrscheinlichkeit das mindestens 2 Schüler ein Handy besitzen.
Die Trefferwahrscheinlichkeit beträgt 1/9.
Laut Lösungsbuch kommt bei a 9,48%raus und bei b 66,81%.
Meine Frage wäre wie ich das mit der Bernoulli Formel berechnen kann ?
3 Antworten

Bei a brauchst Du keine Binomialverteilung, sondern Du kannst einfach 8/9^20 rechnen. Denn 8/9 ist die Wahrscheinlichkeit, daß einer kein Handy hat (1-1/9). Das alle keines haben, heißt der erste nicht und der zweite nicht... 20. nicht. Und diese Wahrscheinlichkeiten mußt Du multiplizieren . Bei b) brauchst Du die Binomialverteilung. Formel (n über k)* p^ k * (1-p)^(n-k). Du rechnest zuerst die Wahrscheinlichkeit, daß genau 2 ein Handy haben. Das ist (20 über 2) * (1/9)^2 * (1-1/9)^(20-2). Dann das gleiche für genau 3 und so weiter bis 20. Die Ergebnisse summierst Du dann auf. Das ^ heißt hoch. Es gibt auch einen Rechner, mit dem Du das überprüfen kannst: http://www.arndt-bruenner.de/mathe/scripts/normalverteilung1.htm

Ich benutze für so etwas immer diese Webseite -->
http://matheguru.com/stochastik/164-bernoulli-kette.html
Die verwendeten Formeln werden da mit angezeigt, die Werte dort eingeben und dann die richtige Schaltfläche für die jeweilige Verteilungsfunktion anklicken !
a.)
n = 20
k = 20
p = 9 / 9 - 1 / 9 = 8 / 9
Formel für die obere kumulative Vereilungsfunktion verwenden.
Ergebnis 0,0948 das sind 9,48 %
b.)
n = 20
k = 2
p = 1 / 9
Formel für die obere kumulative Vereilungsfunktion verwenden.
Ergebnis 0,66809 das sind 66,809 % gerundet 66,81 %
------------------------------------------------------------------------------------------------------------
Wie bereits gesagt, die Formel wird auf der Webseite gezeigt ! Aber zur Sicherheit hier noch mal ein Bild von der Formel -->
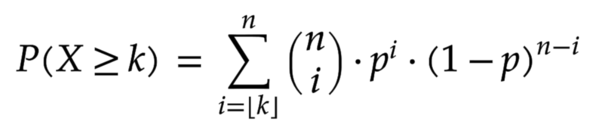

a) n = 20, k = 0 und p = 1/9 in die Binomialverteilung einsetzen und ausrechnen.
b) P(x >= 2) muß berechnet werden. Man kann aber nur P(x=2) oder P(x<=2) berechnen. Deswegen muß man zuerst P(x>=2) umformen. Das funktioniert mit dem Gegenereignis:
P(x>=2)= 1-P(x<2) = 1-P(x<=1) =1-P(x=0)-P(x=1)=1-9,48%-23,71%=66,81%