Fallschirmsprung. Ermittle vI (t) durch Verschieben des Terassenpunktes. Kann jemand die Vorgehensweise bei dieser Aufgabe erklären?
Hallo hat jemand eine Idee wie diese Aufgabe zu lösen ist. Anbei ist noch das Zeit-Geschwindigkeitsdiagramm.
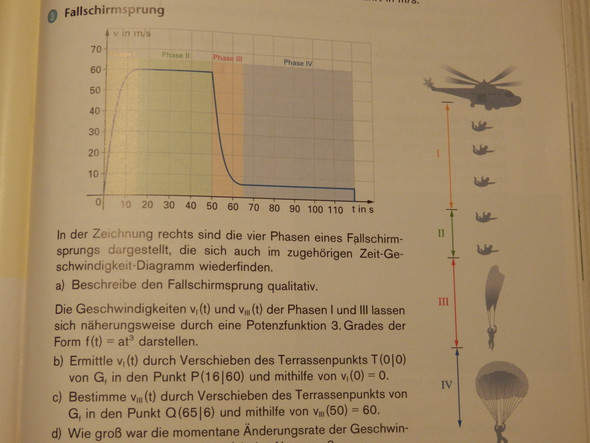
Ein Fallschirmsprung wird in vier Phasen untergliedert. Die Geschwindigkeiten vI (t) und vIII (t) der Phasen I und III lassen sich näherungsweise durch eine Potenzfunktion 3.Grades der Form f(t) = at3 darstellen.
Ermittle vI (t) durch Verschieben des Terassenpunktes T (0Ι0) von Gf in den Punkt P (16Ι60) und mithilfe von vI (0) = 0.
Danke für Eure Vorschläge :-)
2 Antworten
Es fängt damit an dass Du Deine Parabel dritten Grades im Koordinatensystem nach rechts verschiebst, in dem Du von Deinem Argument etwas abziehst. Zusätzlich addierst Du zum Funktionswert den y-Wert Deines Terrassenpunktes. Das ganze hat folgendes Format
f(t) = a*t^3 --> v(t) = a*(t-t_offset)^3 + v_offset
Dann muss a bestimmt werden. Hier empfehle ich zur Gewinnung einer Bestimmungsgleichung einfach das andere Ende der Kurve zu verwenden. Naheliegend wäre auch eine Bestimmung über die Steigung im Ursprung. Die kann man aber nur graphisch ermitteln und führt leider zu einer schlecht angepassten Kurve.
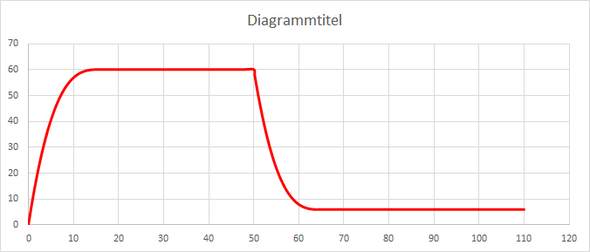
Versuch es selber. Im Bild siehst Du die Lösung, die ich mit Excel nachprogrammiert habe.
Vielen Dank für die schnelle Antwort und die Ausführung :-)
v(t) = a(x-16)³ + s0
v(16) = 60, also s0 = 60.
v(t) = a(x-16)³ + 60
v(0) = 0, also 0 = a(-16)³ +60, also a = 60/16³