Tatsächlich ist Tavor Expidet das einzige Lorazepam-Präparat, das in Schmelztabletten vorliegt. Alle anderen Generika gibt es nur in Tablettenform.

Eine Möglichkeit wäre, auf Lorazepam-Tabletten (z.B. Lorazepam-neuraxpharm oder Lorazepam-ratiopharm) auszuweichen und diese zu mörsern. Das ist bei den meisten Lorazepam-Tabletten möglich (Packungsbeilage beachten) und die typische Alternative bei Betroffenen mit Schluckproblemen bei den immer wieder vorkommenden Lieferschwierigkeiten von Tavor Expidet.

Ansonsten bliebe nur eine Umstellung auf einen anderen vergleichbaren Wirkstoff, der in Form von Schmelztabletten lieferbar ist. Das müsstest du mit deinem Arzt besprechen.

Ich wünsche dir alles Gute.

Man kann es schon logisch lösen, an eine ernst gemeinte Drittklassaufgabe glaube ich aber nicht.

Wir fangen bei der Blase ganz links an und arbeiten uns im Zickzackmuster durch.

Sei x der Wert der Blase ganz links. Dann hat die Blase darunter den Wert x - 90 und die Blase daneben (in der Mitte) den Wert 260 - x. Bringt uns hier hin:

Weiter im Text: Dann hat die Blase rechts unten den Wert



und addieren wir 170 drauf, kommen wir auf den Wert 520 - 2x für die Blase rechts oben. Bringt uns hier hin:

Damit können wir jetzt eine nicht-triviale Gleichung aufstellen, die zum Ziel führt:



Nach x aufgelöst: x = 120

Ab hier lassen sich dann in wirklicher Drittklassmanier die fehlenden Zahlen bestimmen:

Wir haben eine Menge von n (Daten-)Punkten:



Die mittlere lineare Abweichung dieser Menge ist nun die durchschnittliche Abweichung zum Durchschnitt, d.h. der Durchschnitt der Abweichungen zum Durchschnitt. Klingt kompliziert, ist aber eigentlich ganz einfach.

Schritt für Schritt

1. Berechne den Durchschnitt.
2. Berechne für jeden Punkt den Abstand zum Durchschnitt.
3. Berechne den Durchschnitt der berechneten Abstände zum Durchschnitt.
4. Das ist die mittlere lineare Abweichung.

Wir haben folgende Daten:



Davon berechnen wir jetzt die mittlere lineare Abweichung.

Schritt 1: Berechne den Durchschnitt.



Schritt 2: Berechne für jeden Punkt den Abstand zum Durchschnitt, d.h. berechne die Zahl



Das ergibt eine neue Menge:



Schritt 3: Berechne von dieser Menge den Durchschnitt.



Die mittlere lineare Abweichung ist in diesem Fall also genau 4.

Anschaulich ist die mittlere lineare Abweichung einfach die Varianz, wenn man statt zu Quadrieren einfach Beträge nimmt. Damit ist sie genauso wie die Varianz ein Maß für die Streuung einer Menge an Datenpunkten um ihren "Mittelpunkt" (den Durchschnitt). Anders als bei der Varianz fallen große Abweichungen bei der mittleren linearen Abweichung aber nicht überproportional stark (= quadratisch) ins Gewicht, sondern proportional (= linear).

Für a, b ≥ 0 ist



denn: Setze



dann gilt



und bildet man den Limes auf beiden Seiten, ergibt sich die Behauptung mit dem Sandwichlemma.

Das nennt man den ternären Operator.

Vor dem Fragezeichen steht eine Bedingung, danach zwei Ausdrücke, getrennt durch einen Doppelpunkt. Ist die Bedingung wahr, wird der erste Ausdruck ausgewertet, sonst der zweite.

Beispiele:

function getAgeCategory(age) {
  return age >= 18 ? "volljährig" : "minderjährig";
}

function getParity(number) {
  return number % 2 == 0 ? "gerade" : "ungerade";
}

function getSecretData(isAuthorized) {
  return isAuthorized ? secretDataService.getSecretData() : null;
}

Mit dem Ausrufezeichen, das zum Beispiel in != vorkommt, hat das nichts zu tun.

Unendlich ist ein künstliches mathematisches Konzept. Dieses (wie in deinem Auto-Beispiel) auf den realen Alltag zu übertragen, geht in der Regel schief.

Um das Konzept verschiedener Unendlichkeiten zu verstehen, sollten wir uns Unendlich nicht als Zahl, sondern besser als Anzahl vorstellen.

Der Begriff der Anzahl ist natürlich eng mit der Mengenlehre verbunden: Wir verstehen eine Anzahl als Anzahl der Elemente einer Menge. Im Folgenden werden wir diese Idee formal präzisieren.

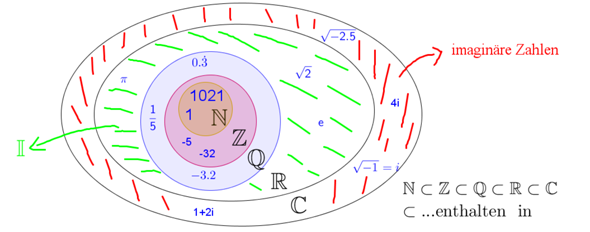
Alles beginnt mit der Menge der natürlichen Zahlen IN, die "vom Himmel fällt" (präziser: axiomatisch postuliert wird) und in der die Zahlen 1, 2, 3, 4, 5, usw. enthalten sind. Alles Weitere wird auf Basis der natürlichen Zahlen formal präzise aufgezogen.

Wir gehen in zwei vor:

1. Definition: Was ist eine endliche Menge und was eine unendliche Menge?
2. Definition: Wann sind zwei Mengen gleich groß?

Ich werde das an dieser Stelle nicht streng formalisieren, denn die Intuition genügt: Eine Menge ist endlich, wenn wir alle Elemente nacheinander aufschreiben können und irgendwann fertig werden. Eine Menge ist unendlich, wenn sie nicht endlich ist.

Eine unendliche Menge ist also einfach eine nicht-endliche Menge. Das trennt die Mengen bezüglich der Anzahl schon mal in zwei Gruppen auf. Wir werden sehen, dass wir die Gruppe der unendlichen Mengen in noch feinere Teilgruppen auftrennen können.

Zunächst wollen wir definieren, wann zwei Mengen als gleichmächtig (sozusagen gleich groß) gelten sollten und zwar wie folgt: Zwei Mengen seien gleichmächtig, wenn jedem Element der einen Menge eindeutig ein Element der anderen Menge zugeordnet werden kann, sodass (und das ist der wesentliche Punkt) jedes Element beider Mengen genau einen Partner in der anderen Menge hat, d.h. diese Zuordnung umfasst alle Elemente beider Mengen.

Formal: Zwei Mengen sind gleichmächtig, wenn eine sog. Bijektion zwischen beiden Mengen existiert.

Damit sind die Menge der ungeraden Zahlen und die Menge der geraden Zahlen gleichmächtig - wir können einfach jeder ungeraden Zahl ihren Nachfolger (dieser ist gerade) zuordnen, d.h. der 1 die 2, der 3 die 4, der 5 die 6, usw. An dieser Stelle sollte man kurz innehalten und sich klar machen, dass diese Zuordnung tatsächlich die oben genannten Bedingungen (hier in umgekehrter Reihenfolge aufgelistet)

1. Jedes Element beider Mengen hat einen Partner.
2. Dieser Partner ist eindeutig.

genügt.

Genauso sind die Menge aller natürlichen Zahlen und die Menge der geraden Zahlen gleichmächtig. Das mag erstmal kontraintuitiv erscheinen, da die Menge der geraden Zahlen offensichtlich eine echte Teilmenge der natürlichen Zahlen ist und damit rein intuitiv "kleiner" sein sollte. Per Definition sind die beiden Mengen aber gleichmächtig (auch das sollte man sich kurz klarmachen) und es wird gleich Schritt für Schritt klar werden, warum diese Definition von "gleichmächtig" für die Idee von "gleichgroß" die einzig sinnvolle ist.

Allerdings sind die natürlichen Zahlen nicht gleichmächtig zur Menge der reellen Zahlen. Der Beweis hierfür ist etwas komplizierter, sodass ich ihn hier nicht ausführen werde, aber man kann zeigen, dass eine Zuordnung zwischen IN und IR nie beide oben genannten Eigenschaften gleichzeitig erfüllen kann - ist eine der beiden Eigenschaften erfüllt, kann die andere nicht mehr erfüllt sein.

Das zeigt, dass zwei unendliche Mengen nicht zwingend gleichmächtig sein müssen. Es gibt also verschieden große unendliche Mengen...

Und genau daher rührt der Begriff verschiedener Unendlichkeiten. Unendlich ist der Oberbegriff und bedeutet schlicht nicht-endlich, aber nicht jede Unendlichkeit ist vergleichbar (im Sinne einer Elementanzahl einer Menge bzw. der Mächtigkeit). Das erlaubt, die Gruppe der unendlichen Mengen in Teilgruppen einzuteilen, wobei jede Teilgruppe aus allen gleichmächtigen unendlichen Mengen besteht. Die Teilgruppen nennt man Kardinalzahlen (wobei die Bezeichnung "Zahl" hier irreführend ist, denn es handelt sich bei einer Kardinalzahl um eine Menge von Mengen).

Für Kardinalzahlen verwendet man in der Mathematik üblicherweise hebräische Buchstaben. Die Gruppe der zu IN gleichmächtigen Mengen bezeichnet man beispielsweise als Aleph-0 (mit dem hebräischen Buchstaben Aleph), die Gruppe der zu IR gleichmächtigen Mengen mit Aleph-1.

Man kann sich nun noch weitere Dinge überlegen, die an dieser Stelle allerdings zu weit führen würden. Zum Beispiel, ob es eine Kardinalzahl zwischen Aleph-0 und Aleph-1 gibt (also eine Menge, deren Mächtigkeit größer als die von IN, aber kleiner als die von IR ist). Wer interessiert ist, kann sich mal die Kontinuumshypothese anschauen, diese beschäftigt sich genau mit dieser Frage.

Zusammengefasst:

• Unendlich bedeutet nicht-endlich.
• Gleichmächtig (= "gleich groß") bedeutet elementweise gegenseitig eindeutig und vollständig zuordenbar.
• Es gibt unendliche Mengen, die nicht gleichmächtig sind.
• Gruppen gleichmächtiger Mengen bezeichnet man als Kardinalzahlen.
• Die Kardinalzahlen unendlicher Mengen beschreiben genau die "verschieden großen Unendlichkeiten".
• Eine Übertragung dieses Unendlichkeitskonzepts auf den Alltag ist in der Regel nicht möglich.

Liebe Grüße.

Zur Vereinfachung betrachten wir einen Definitionsbereich, in dem die Funktion tan bijektiv ist, ansonsten müssten wir uns mit Perioden herumschlagen.

Wir können direkt



und damit



schreiben.

Alternativ verwenden wir die Doppelwinkelformel



und erhalten damit



was elementar nach tan(a/2) umgeformt werden kann.

Damit du deinen Code direkt ausführen kannst, benötigst du die main-Methode:

public class Vokale {
    public static void main(String[] args){
        // auszuführender Code
    }
}

Code, der direkt in eine Klasse gesetzt wird, aber die Klasse nicht definiert, ist syntaktisch falsch. Inhaltlicher Code gehört in eine Methode wie die main-Methode.

Warum es mit den zusätzlichen geschweiften Klammern funktioniert, ist vielleicht etwas zu viel für den Anfang, ich erkläre es aber trotzdem: Wird in einer Klasse auf Methodenebene ein einfacher Block gesetzt, wird dieser als sog. instance initialization-Block interpretiert. Dieser kann inhaltlichen Code enthalten und wird immer dann ausgeführt, wenn die Klasse initialisiert wird, sogar noch vor dem Konstruktor. Es ist also eher ein nicht beabsichtigter Zufall, dass der Code in diesem Fall tatsächlich syntaktisch korrekt ist.

Mehr dazu hier: https://www.baeldung.com/java-static-instance-initializer-blocks

Klar. Bestimme für beide Vektoren jeweils eine Gerade, die zum jeweiligen Vektor senkrecht steht und diesen in der Mitte schneidet. Der Schnittpunkt der Geraden ist der Umkreismittelpunkt, der Abstand zu den Fußpunkten der Vektoren der Umkreisradius.

Es ist



wobei im ersten Schritt genutzt wurde, dass Exponenten vorgezogen werden können, d.h. dass



ist und anschließend nur noch grundlegend zusammengefasst wurde.

Du musst die Rechnung klammern.

Der Compiler arbeitet bei Addition ohne Klammerung von links nach rechts. Er interpretiert das Plus nach dem String nicht als mathematische Addition, sondern als String-Konkatenation (wie es ja auch gemeint ist). Er konkateniert also "Das Ergebnis ist: " mit a. Dann versucht er, von dem sich ergebenden String b abzuziehen. Das funktioniert natürlich nicht.

Wenn du die Rechnung klammerst, berechnet er erst die (mathematische) Subtraktion und addiert (= konkateniert) es dann zu dem vorhergehenden String.

System.out.println("Das Ergebnis ist: " + (a - b));

So ist es.



konvergiert nur für |q| < 1.

Für q = 5 gilt



und die Reihe divergiert.

Das gilt allerdings nur für die Reihe und nicht für die Summe. Für die geometrische Summe gilt für q = 5 trotzdem, dass



ist. Für N → ∞ ergibt sich nur keine Konvergenz.

Per üblicher Definition nicht.

Die reellen Zahlen enthalten die rationalen Zahlen und die irrationalen Zahlen. Alle Zahlen, die zu den reellen, aber nicht zu den rationalen Zahlen gehören, sind irrational.

Die komplexen Zahlen sind dann eine Obermenge der reellen Zahlen. Irrationale Zahlen sind aber per Definition reell.

Quelle: https://3.vobs.at/maturawiki/index.php/Zahlenmengen

Hier in grün die irrationalen Zahlen. IR wird gebildet aus der blauen Menge (den rationalen Zahlen) und der grünen Menge (den irrationalen Zahlen).