Wie geht die Ableitung von Log Funktionen?
Hallöchen, ich hätte da mal 'ne Frage und zwar schreibe ich morgen eine Mathe Klausur und mir ist eins immer noch nicht klar geworden.
Im Anhang befindet sich ein Bild zu einer Log. Fkt. und es wäre nett, wenn mir jemand dabei helfen könnte diese, bzw. grundsätzlich Log. Funktionen abzuleiten.
Ich bin mir nicht sicher ob ich da die Kettenregel benutzen muss und wenn, dann auch nicht genau wie.
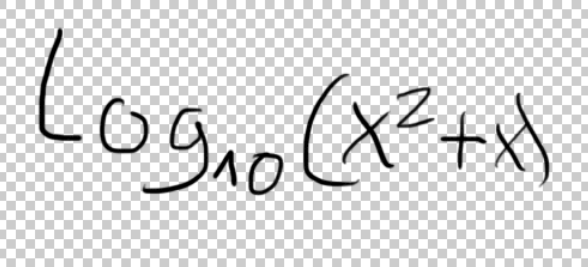
Einfach nur schnell hingekríckelt :)
4 Antworten
f(x) = log_10(x ^ 2 + x)
Das kannst du umschreiben :
f(x) = (1 / ln(10)) * ln(x ^ 2 + x)
ln(...) = natürliche Logarithmusfunktion
Kettenregel :
Innere Funktion :
u(x) = x ^ 2 + x
Innere Ableitung :
u´(x) = 2 * x + 1
Äußere Funktion :
v(x) = ln(u(x))
Äußere Ableitung :
v´(x) = (1 / u(x))
Für u(x) das einsetzen für das u(x) steht :
v´(x) = (1 / (x ^ 2 + x))
Faktor :
(1 / ln(10))
Faktor mal innere Ableitung mal äußere Ableitung :
f´(x) = (1 / ln(10)) * (2 * x + 1) * (1 / (x ^ 2 + x))
Das kannst du noch vereinfachen :
f´(x) = (2 * x + 1) / (ln(10) * (x ^ 2 + x))
Du solltest dir in deinem Beispiel die Kettenregel und die Faktorregel anschauen.
Ich zeige nur die Herleitung:
f(x) = log_a(x) = f‘(x) = (1)/(In(a) * x))
Umschreiben durch Basiswechsel Satz :
u soll freie Basis sein :
Definition des Logarithmus:
a^x = b I mit u
log_u(a^x) = log_u(b) I 3. Logarithmus Gesetz
x * log_u(a) = log_u(b)
x = (log_u(b))/(log_u(a))
Basiswechsel Satz :
Mit In bzw. In_e gilt :
log_a(x) = (In(x))/(In(a))
f(x) = (1)/(In(a)) * In(x)) I brechen
f‘(x) = (1)/(In(a) * 1/x I Faktorregel und In(x)
f‘(x) = (1)/(In(a)*x)
Beispiel:
f(x)=log_2(5x) oder In(5*x)/(In(2)
bzw 1/In(2) * In(5*x)
f‘(x) = 1/In(2) * 1/5*x * 5
f‘(x) = (1)/(In(2) * x)
Integration bringt :
∫ (1)/(In(2)*x) dx I brechen
∫ (1)/(In(2)) * 1/x dx I Faktor rausziehen
(1)/(In(2) ∫ 1/x dx I Integration
(1)/(In(2)) * In(x) + C , C € IR
[(In(x))/(In(2))] + C
log_2(x) mit c = log_2(5) gilt nach
log_a(u) + log_a(v) = log_a(u*v)
log_2(x) + log_2(5) = log_2(5*x)
Die Ableitung eines Logarithmus von x zur Basis n ist
1/(x*ln(n))
Dann brauchst du nur noch die Kettenregel.
ich kenne nur die Ableitung bomb natürlichen Logarithmus, die ist 1/x und dann müsste das mit Kettenregel gehen ganz normal.
Aber wie das mit 10er Logarithmen ist keine Ahnung