Was mache ich bei der Ableitung dieser natürlichen Logarithmus-Funktion nur falsch?
Hallo Mathe-Experten,
an folgender Aufgabe (Ableitung einer natürlichen Logarithmus
funktion) bin ich gerade am verzweifeln.
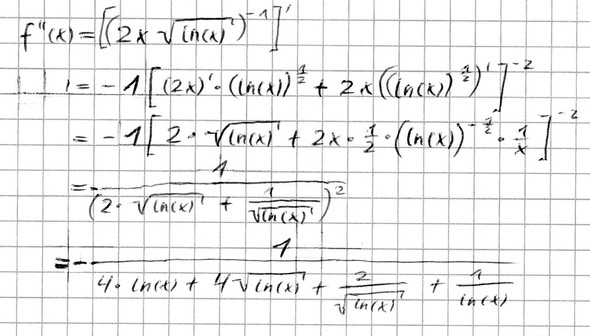
Trotz meiner Meinung nach korrekter Anwendung der Kettenregel erhalte ich ein falsches Ergebnis.
So: Bilder sagen mehr als 1000 Worte!
Danke und Gruß carbonpilot01
2 Antworten

Also ich nehm mal an dass deine abzuleitende Funktion f'(x)=(2xsqr(ln(x)))^(-1) ist
dann hast du hier bei der kettenregel ein paar fehler, irgendwie hast du da äussere und innere ableitung durcheinander gebracht.
zr info: wenn ich nachfolgend irgendwas schreibe wie (...)' dann ist gemeint dass hier die ableitung dessen stehen soll, was in der klammer ist. was das genau ist berechnen wir erst danach. wir gehen das schrittweise an da es sonst zu umfangreich ist.
es ist:
äusserste ableitung:
(-1)*(2xsqr(ln(x)))^(-2)
die innere ableitung ist nach Produktregel:
(2xsqr(ln(x)))'=(2)*sqr(ln(x))+(2x)*(sqr(ln(x))'
nun ist desweiteren, wieder mit kettenregel:
(sqr(ln(x)))'=((ln(x))^(1/2))'=((1/2)*ln(x)^(-1/2))*(1/x)
das (1/x) rechts ist die innere ableitung, alles andere gehört zur äusseren ableitung.
damit ist die anfangs erwähnte innere ableitung:
(2xsqr(ln(x)))'=(2)*sqr(ln(x))+(2x)* (sqr(ln(x))'
=(2xsqr(ln(x)))'=(2)*sqr(ln(x))+(2x)* [((1/2)*ln(x)^(-1/2))*(1/x)]
insgesamt ergibt sich also:
f''(x)
=[f'(x)]'
[(2xsqr(ln(x)))^(-1)]'
=[(-1)*(2xsqr(ln(x)))^(-2)]*[(2)*sqr(ln(x))+(2x)*(sqr(ln(x))']
=[(-1)*(2xsqr(ln(x)))^(-2)]*[(2)*sqr(ln(x))+(2x)*[((1/2)*ln(x)^(-1/2))*(1/x)]]
und ja, es sieht grottenhässlich aus wenn man es hier auf dem computer schreibt.
daher schreib es am besten ab, natürlich schön als brüche und wurzeln und so.
und guck was man noch kürzen oder vereinfachen kann.
So zur allgemeinen Erklärung:
Im Prinzip benutzt du bei der Kettenregel eine Art Substitution.
Ich zeig dir mal am Beispiel was ich meine:
(sqr(ln(x)))' sei gesucht.
wir wählen nun, da es sich halt anbietet, die substitution u=ln(x).
dann ist (sqr(ln(x)))'=(sqr(u))'
grundaussage der kettenregel ist dann
(sqr(ln(x))) nach x abgeleitet ist das selbe wie
sqr(u) nach u abgeleitet mal u nach x abgeleitet
aka d(sqr(u))/du*du/dx
es ist
d(sqr(u))/du=(1/2)*u^(-1/2)
und
du/dx=(ln(x))'=1/x
dann ist
(sqr(ln(x))'=[(1/2)*u^(-1/2)]*(1/x)
natürlich können wir u da nicht drinstehen lassen, soll ja schließlich alles in abhängigkeit von x sein.
Darum setzen wir einfach unseren term für u wieder ein (auch genannt "rücksubstitution"):
(sqr(ln(x))'=[(1/2)*(ln(x))^(-1/2)]*(1/x)
und so funktioniert das immer.
sagen wir, du hast was grottenhässliches wie
f(x)=sin(ln(x^3))
dann machst du die folgenden substitutionen:
a=sin(b)
b=ln(c)
c=x^3
dann ist f'(x) einfach
f'(x)=da/db*db/dc*dc/dx
d.h. du musst diese 3 ableitungen berechnen und miteinander multiplizieren.
Im ergebnis, das du dann erhältst, setzt du dann solange c in b und b n a ein, bis da nur noch x als variable vorkommt.
Und zack hast du dein ergebnis!
oben bei der aufgabe war das gleiche prinzip, nur musstest du da bei den ableitungen noh produktregel anwenden, es kamen wurzel und ln vor, deren ableitung in zeilenschreibweise schon ziemlich hässlich ist.
Und ja, im normalbetrieb schreibt man sich nicht wirklich die substitutionen hin, sondern leitet bspw. nach ln(x) ab (indem du ln(x) einfach mal so als festen klotz hinnimmst nach dem du ableitest. dass der in einer anderen ableitung noch nach x abgeleitet wird, ist unerheblich.)

quotientenregel wäre übrigens auch möglich gewesen wenn du es als 1/(2xsqr(ln(x))) schreibst

Ich versuch's auch mal.
f(x) = (2x √(ln x))⁻¹ = (1/2)* x⁻¹ * (ln x)^(-1/2)
In dieser Schreibweise finde ich es leichter, mit Produkt- und Kettenregel die Ableitung durchzuführen.
u = (1/2) * x^(-1) u' = (- 1/2)x^(-2)
v = (ln x)^(-1/2) v' = (-1/2) * (ln x)^(-3/2)*(1/x)
innere Ableitung ist (1/x)
uv' = (-1/4)* x^(-2) * (ln x)^(-3/2)
vu' = (-1/2)* x^(-2) * (ln x)^(-1/2)
Das muss ich noch addieren:
f'(x) = ((-2 * ln x) - 1) / (4 x² (ln x)^(3/2)
= - [(1 + 2 ln x)/(4x² (ln x)^(3/2)]
Ich hoffe, es ist mir gelungen, alles fehlerlos von meinem Zettelchen zu übertragen. Einige Zwischenergebnisse habe ich weggelassen. Nachlieferung möglich.
Ich meine, mit u und v fährt man immer noch am besten.

Vielen lieben Dank. Ich habe es jetzt selbstständig gelöst ;-)