Was bedeutet dieses Zeichen bei der Integralrechnung?
Was will mir dieses Zeichen sagen. Ich kanns halt nicht mal googlen, weil ich den Namen nicht kenne und ich das Zeichen nicht mit meiner Tastatur eingeben kann.
Gemeint ist der lange, gebogene Strich
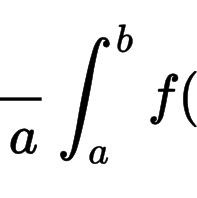
8 Antworten

Wenn du Ableiten kennst, kannst du (zum Teil auch) integrieren.
Die Schreibung ist allerdings mit einigen Formalismen behaftet, die man erst begreift, wenn das Integrieren in der Schule drankommt.
Trivial betrachtet, geht es so:
f(x) = x² f '(x) = 2x
Dann ist ∫ 2x dx = x² Andere Sperenzchen lassen wir mal weg.
Man liest es: Integral von 2x dx gleich x Quadrat
Das Integrieren ist also ein Umkehren des Ableitens.
Erinnere dich mal an den Anfang der Wurzelrechnung. Da hast du zunächst auch nur gewusst, dass √9 = 3
ist, weil 3² = 9
Die weitergehenden Erkenntnisse kamen später hinzu.
Das wird bei der Integration nicht anders sein.

Dann kommt hier als Nachschlag noch die Sache mit den Grenzen a und b.
3
Steht da ∫ 2x dx , dann heißt es, dass du aus x² eine Differenz
1
machst in der Form 3² - 1² = 8 F.E.
Das sind Flächeneinheiten (meist also cm²). Und das ist exakt die Fläche unter dem Integranden 2x (Gerade) bis hin zur x-Achse, und zwar in dem Intervall von 1 bis 3.

Das Integralzeichen. Dass es ein wenig wie ein »S« aussieht, ist kein Zufall, da das Integrieren vom Summieren »abstammt«. Nach Riemann wird eine Funktion gedanklich durch eine Folge von Treppenfunktionen fₙ moduliert, die in Intervallen xₖ einer festen Breite
(Δx)ₙ = (b – a)/n
konstant sind und sozusagen immer schmaler werden:
∑_[k=1]^{n} (Δx)ₙ·fₙ(xₖ) → ∫_[a]^{b} dx f(x).
Lebesgue leitet einen anderen Integralbegriff mit Hilfe des Lebesgue'schen Maßes über die sogenannten Einfachen Funktionen her, bei denen die Breite nicht fest ist.

Mit Hilfe einer Bildschirmtastatur kann man das Integralzeichen ∫ eingeben.
Da ich Windows selten verwende, weiß ich nicht, wie entsprechende Programme heißen. (ich verwende Linux → hier "onboard").
Weiters gibt es in Linux eine "Zeichentabelle", wo für jede (installierte) Schriftart alle möglichen Zeichen stehen und diese per Klick eingefügt werden können, zB: ∫ ∪ ≅ ...
Vielleicht gibt es sowas auch für Windows

Für Handy (Android; Apple hab ich nicht, weiß daher auch nix Genaues) gibt es Tastatur-Apps mit Sonderzeichen (und auch anderen Sprachen). Ich verwende "AnySoftKeyboard", das diverse Tastaturen (Deutsch, Englisch, Griechisch, Mathe,....) anbietet, die per Tastendruck einfach zu wechseln sind.

Das bedeutet einfach, dass ein Integral folgt, also die Fläche unter der folgenden Funktion von der x-Stelle a bis zur x-Stelle b berechnet werden soll.

Das ist das Zeichen für ein Integral.
https://de.wikipedia.org/wiki/Integralzeichen
das a und b sind die Grenzen des Integrals und somit handelt es sich hierbei um ein bestimmtes Integral.


Die Funktion im Integral integrieren und in den gegebenen Grenzen auswerten.
Ganz normale Integralrechnung eben, das lernt ihr normal in der Schule sobald ihr es braucht.

Das mit dem integrieren ist eine Sache für sich, vor allem wenn die Funktionen kompliziert sind.

Nur mit dem Algebraischen Integrieren, Runge Kutta Verfahren und man kann beinahe jedes Integral in kurzer zeit nummerisch lösen ;)
Bin am Handy