Primzahltest Algorithmus?
Hallo zusammen,
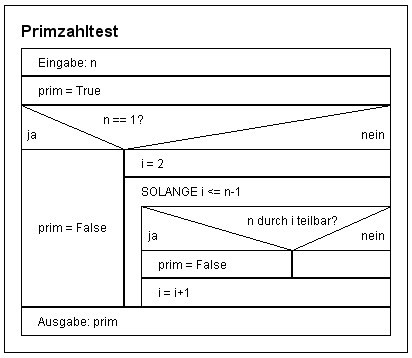
Und zwar muss ich einen Informatik Vortrag ausarbeiten und habe einen Übungsalgorithmus dazu bekommen ( Thema ist: Korrektheit von Algorithmen), das Bild des Algorithmus befindet sich im Anhang. Das Problem ist dies ist mein erstes Jahr Informatik, den Wechselwegnahme Algorithmus konnte ich noch verstehen, aber bei dem Primzahltest komm ich leider nicht weiter.
Es wäre schön, wenn mir jemand weiterhelfen könnte. danke :)
LG
2 Antworten
Eine natürliche Zahl heißt bekanntlich eine Primzahl genau dann, wenn
- sie größer als 1 ist
- sie außer 1 und sich selber keine weiteren Teiler hat (die natürliche Zahlen sind)
Es geht also darum, nachzuweisen, dass der Algorithmus auf diese Bedingung prüft (oder auf eine mathematisch äquivalente Bedingung - das ist dann aber aus dem Gebiet der Mathematik und nicht mehr der Informatik).
Den Kode halte ich für zwar formal richtig....aber nicht nach Defeinition.
Korrekt wäre es, wenn du eine Schleife bildest von 2 bis Prüfzahl/2. Daran zählst du wie oft sich die Zählervariable durch die Prüfzahl mit Rest 0 teilen lässt. Wenn du GENAU 0 Ergebnisse findest, dann hast du eine Primzahl?
Warum nur bis Prüfzahl/2? Nun: 101/52 ist 1. 101/53 ist auch 1. Die Zahlen nach der Hälfte haben ALLE einen Rest. Ab Prüfzahl+1 hast du Ergebnis immer 0
Rein theoretisch müsstest du von 1 bis Prüfzahl laufen und genau 2 Ergebnisse finden um eine zahl als Primzahl zu verifizieren. So ist die Primzahl jedenfalls definiert: GENAU 2 Teiler.
Jedoch ist der Teiler 1 und Prüfzahl selbst irgendwie logisch. Daher lässt du es einfach von 2 bis Prüfzahl/2 laufen. Findest du einen Teiler kannst du die Schleife abbrechen
Also ist sozusagen das einzige was der Algorithmus mir sagt, ob eine beliebige natürliche Zahl eine Primzahl ist?