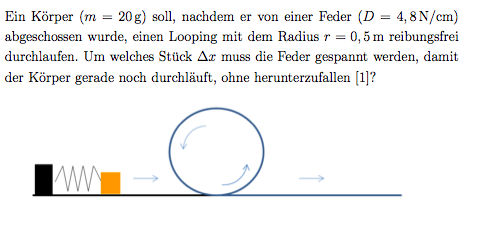
Physik - potentielle und kinetische Energie?
Bei der Aufgabe bekomme ich 3.2 m raus, was mir aber ziemlich unrealistisch erscheint. Kann mit da jemand den Lösungsweg hinschrieben? Danke!
2 Antworten

Ich hätte jetzt erstmal gefordert, dass die Zentripetalkraft gleich der Gravitationskraft ist für den Punkt ganz oben. (w ist jetzt mal Omega für Kreisfrequenz ;) )
w^2*r*m=m*g mit v_oben = w*r
dann die Geschwindigkeit bestimmen, die dass Teil oben haben muss.
Zu der Geschwindigkeit kommt dann die Geschwindigkeit hinzu die es beim steigen verliert. Also E_unten = E_oben + E_pot = 1/2*m*v_oben^2+2*r*g*m
Dann über E_unten = 1/2*m*v_unten^2 die untere Geschwindigkeit bestimmen.
E_unten=E_Feder=int c*s*ds = 1/2*c*s^2 damit sollte man dann auf die Spannung der Feder kommen.

Formeln siehe Mathe-Formelbuch
1.Schritt : alles in SI-Einheiten umwandeln (internationale Einheiten)
m=20 g=0,02 Kg und d=4,8 N/cm=480 N/m
1 .Federenergie Ef=1/2 *D * s^2 mit s= (de)x
2.Zentrifugalkraft Fz=m * v^2/r=m * w *r
3. Gewichtskraft Fg=m * g
Am oberen Kreis gilt Fz=Fg ergibt m *v^2/r= m *g ergibt V^2=g *r
V=Wurzel ( g * r)=wur(9,81 m/s^2 * 0, 5 m)=2,2147 m/s
Nun der Energieerhaltungssatz
Ekin=Ef mit Ekin= 1/2 * m * V^2=1/2 *D * (de)x^2
mit V^2=g *r
m * g * r = D * (de)x^2
(de)x=wurzel( m * g * r/D)=wur( 0,02 kg * 9,81 m/s^2 * 0,5 m/480 N/m)=
0,0142959 m = 1,429..cm
Die Feder muss um 1,429 . cm gespannt werden,damit es funktioniert.

keine Ahnung 1. Mit v= wurzel(g *r)= 2,021.. m/s
vielleicht hab ich mich verrechnet !
Evtl hab ich' überlesen, aber ist die Lageenergie im oberen Punkt berücksichtigt worden? Hab 3,2 cm raus.