Fallen auch am Mond alle Körper gleich schnell?
3 Antworten
Ja der Ortsfaktor auf dem Mond ist jedoch ein anderer. Leiten wir uns das ganze theoretisch formal her, dann siehst du es auch selbst.
zu Lebzeiten, formulierte Isaac Newton das Gravitationsgesetz:

G ist die Gravitationsfaktor. also ein Proportionalitätsfaktor. Sollte dir der Begriff neu sein, dann empfehle ich dir das Thema "Lineare Gleichungssysteme" in der Mathematik nochmal anzuschauen. Der Proportionalitätsfaktor entspricht der Steigung einer linearen Funktion.
Im Grunde sagt uns das Gravitationsgesetz, dass die anziehende Kraft F die auf beide Massen m gleichermaßen wirkt quadratisch zum Abstand der Massen r abnimmt.
Die Erde ist ein Planet des Sonnensystems und sein Radius beträgt 3671km. Die Entfernung r im Gravitationsgesetz bezieht sich auf das Masse Zentrum der Massen. Das hat Symmetriegründe, denn der Radius r darf nicht winkelabhängig sein. Aus dem Grund muss die Gravitation eine radiale Kraft sein und neigt zur Kugelform, da hier die Symmetriebedingung erfüllt ist.
nun ziehen wir die variablen G, m und r aus der Gleichung. Wie du erkennen kannst ist der Radius der Erde recht gewaltig. da machen 100m oder gar 1000m kaum einen eindrucksvollen Unterschied. aus dem Grund nehmen wir den Radius r als konstant an. Daraus folgt, dass alle 3 variablen konstante sind (für kleine Höhenunterschiede). aus diese 3 variablen berechnen wir nun eine neue Konstante die wir "Ortsfaktor g" nennen. Auf der Erde wird sie auch "Erdbeschleunigung" genannt:

Es bleibt für die Gewichtskraft:
F=m*g
übrig. wir sehen für den Ortsfaktor geht es bei Planeten vor allem um die Masse und den Radius. Da die Masse und der Radius
des Mondes eine andere ist werden wir auch für den Ortsfaktor g etwas anderes rausbekommen. Machen wir also die gleiche Rechnung für den Mond:

befinden wir uns auf einer Höhe h die relativ klein im Gegensatz zum Planetenradius ist, gilt für die potentielle Energie Epot im Gravitationsfeld:
Epot=m*g*h
im freien Fall wird die gesamte potentielle Energie in kinetische Energie umgewandelt. Wir können die kinetische Energie und Potentielle Energie gleichsetzen:
Epot=Ekin
m*g*h=(1/2)*m*v^2
nach v umstellen:
v=√(g*h*2)
wir sehen, dass sich die Masse aus der Gleichung rauskürzt. das gilt für den Mond genauso wie für die Erde. solange wir vom Abstand her nah an der Oberfläche des Planeten bleiben ansonsten schleicht sich der Faktor r^2 ein und wir müssen integrieren und wir hätten so etwas wie:
W=G*m1*m2∫(1/r^2)*dr
für die verrichtete Arbeit im Gravitationsfeld.
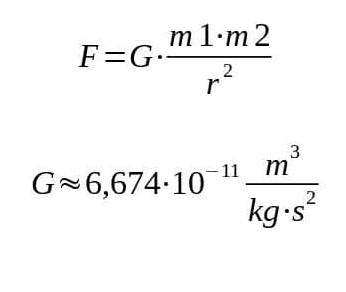


An für sich JA.
Im Schwerfeld werden alle Körper (theoretisch) gleichermaßen beschleunigt. Allerdings schaffen "schwerere Körper" es sich leichter ihren Weg vorbei an Atomen und Molekülen zu bahnen, weshalb auf der Erde nicht alle Körper gleich schnell fallen.
Auf dem Mond gibt es nahezu perfektes Vakuum, die Teilchendichte im Weltall ist im Mittel seeeehr gering. Daher lässt sich das Prinzip sehr gut dort zeigen.
Natürlich, die Schwerkraftgesetze sind universell, gelten überall.