Warum ergibt a^5 am Ende der Zahl immer a?
Hallo zusammen,
ich hoffe ihr versteht meine Frage. Lasst es mich an einem Beispiel noch einmal klarer darstellen:
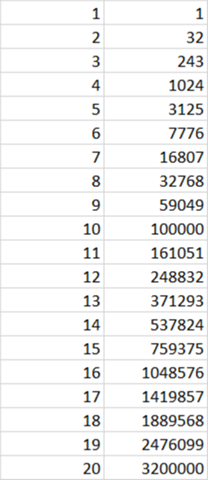
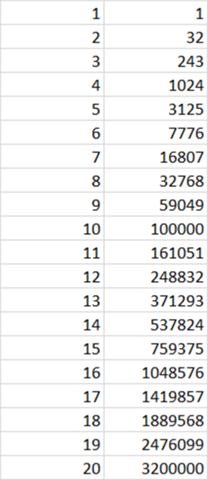
Rechnet man 2^5=32 (endet mit 2)
Rechnet man 16^5=104876 (endet mit 6)
Rechnet man 24^5= 7962624 (endet mit 24)
Usw.
Mich würde interessieren, ob es dafür eine mathematische Erklärung oder Ähnliches gibt?
LG
4 Antworten

Das ist Zufall bzw. liegt daran, dass du es mit so kleinen Zahlen ausprobiert hast.
Gegenbeispiel: 32.146^5 = 34.326.909.247.918.475.250.976, da ist zwar die 6 da, die Einerstelle, aber der Rest nicht.
Speziell bei der Einerstelle ist es aber tatsächlich kein Zufall.
Wenn du dich an die Rechenregeln für die schriftliche Multiplikation aus der Grundschule erinnerst, dann siehst du, dass die Einerstelle eines Produkts nur von den Einerstellen der Faktoren abhängt, und damit hängt auch die Einerstelle einer Potenz nur vom Exponenten und der Einerstelle der Basis ab.
Die 1 bleibt eine 1.
Bei 2 gibt es eine Rotation: 2, 4, 8, 6, 2
Bei 3 gibt es ebenfalls eine Rotation: 3, 9, 7, 1, 3
Bei 4 ebenfalls, es ist dieselbe wie bei der 2, nur einen Schritt weiter hinten einsteigend.
5 bleibt 5.
6 und 8 dieselbe Rotation wie bei 2, mit anderem Einstieg, 7 und 9 sind in der Rotation der 3 enthalten.
Es gibt also nur 2 Zyklen, beide haben die Länge 5. Das hängt damit zusammen, dass die 5 als Faktor in der Basis (10) unseres Zahlensystems enthalten ist.

Ja, genau darum ging es mir, dass die letzte Zifffer immer die gleichen ist wie die letzte von a. Danke für deine Antwort

Wenn du es ganz abgefahren willst, dahinter steckt der Satz von Euler: https://de.wikipedia.org/wiki/Satz_von_Euler
Oder hier in der Version a^(Phi(10)+1) = a (mod 10).
Phi(10) ist die Anzahl der zu 10 teilerfremden Zahlen <= 10, also 4 .
Das heisst, a hoch 5 lässt bei Division durch 10 den Rest a. Ist a nur einstellig, dann passt das zu deiner Beobachtung.

Coole Beobachtung. Und ja, das kann man natürlich beweisen - für die letzte Ziffer. Für mehr als die letzte Ziffer gilt das allgemein nicht, aber das hast du ja schon selbst herausgefunden.
Annahme: Für jede natürliche Zahl n oder n=0 gilt, dass n und n^5 in der Darstellung im Zehnersystem die gleiche Endziffer haben.
Beweis:
1) Man stellt fest, dass es reicht, für n die Zahlen 0 bis 9 zu zeigen.
2) Dann zeigt man, dass das für die Ziffern 0 bis 9 einzeln gilt - das sind ja nur 10 Fälle.
Beweis zu 1)
Sei n eine natürliche Zahl >= 10. Dann kann man n eindeutig schreiben als n = 10 * a + b mit 0 <= b <= 9 und einer natürlichen Zahl a.
Dann gilt:
n^5 = (10*a + b)^5 = b^5 + Rest
Wobei der Rest immer mindestens einen Faktor (10*a) enthält. Der Rest ist also durch 10 teilbar, hat als keinen Einfluss auf die letzte Ziffer.
Damit hat n^5 dieselbe letzte Ziffer wie b^5.
Beweis zu 2)
Unterscheide die Fälle wie gesagt einzeln und rechne das aus.


Das auch noch: Jede Zahl hoch 5 endet mit der letzten Stelle so wie die letze Stelle der Basis