Mathe quadratische funktionen textaufgabe sos mein leben keinen sinn?
Ich verstehe die aufgabe 4 (bei der 4 soll die scheitelform auch angewendet werden) und 5 nicht :( die lösungen liegen mir vor bei der nummer 4: lösung=5m und bei der nummer 5: lösung=3,42m hinter leo
3 Antworten

zu 4. Aus den Bild sind 3 Punkte erkennbar und somit sind auch 3 Gleichungen mit 3 unbekannte gegeben,also lösbar
f(x)=a2 *x^2+a1 *x +ao
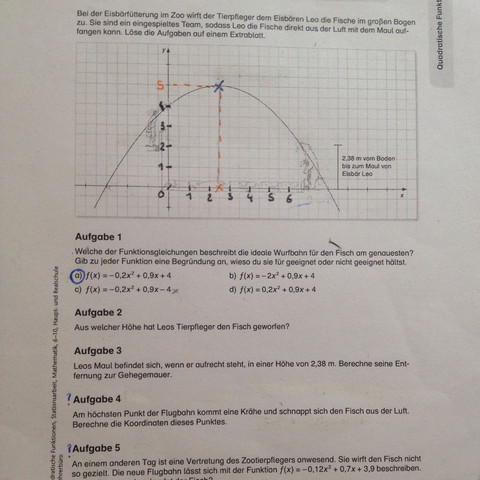
1. a2 *0^2 + a1 *0+ao=4 Punkt des Pflegers P)0/4)
2. a2 *6,5^2 +a1 *6,5 + ao= 2,38 punkt vom Maul des Eisbären P(6,5/2,38)
3. a2 * 2,5^2 +a1 *2,5 +ao=5
hieraus ergibt sich das "lineare Gleichungssystem"
1. 0 *a2 + 0 *a1 +1 *ao=4
2. 42,25 * a2 + 6,5 *a1 + 1 *ao=2,38
3. 6,25 *a2 +2,5 *a1 +1 *ao=5
Lösung : a2=- 0,162 und a1=0,8057 und ao=4
Funktion ist somit f(x)= - 0,162 *x^2 + 0,8057 + 4
Somit ist Formel a) am besten weil Parabel nach unten offen a2=- 0,162 negativ
Scheitelkoordinaten bei x=2,5 und y=4 also ao=4 positiv
und a1=0,80.. liegt nahe bei 0,9

Da du anscheinend nicht 11. Klasse bist ^^:
Scheitelpunktform:
- f(x)= -0.2 x² +0,9x +4
- =-0,2 (x² +0,9x +4)
- =-0,2 ((x-2,25)²-2,25²-20)
- =-0,2 (x-2,25)² +5,0125
Scheitelpunkt ablesbar:
S (-d/e)=>S (--2,25/5,0125)=>S(2,25/5,0125)
(Eigentlich wäre die richtige Gleichung aus dem Bild entnehmbar:
- y=1/3 (x-2,5)² -5
aber nun gut)
5. Aufgabe:
- y=-0,12x² +0,7 x +3,9
- = -0,12 (x² +0,7x/(-0,12)+3,9/(-0,12))
- = -0,12 ( (x- 35/12)² -(35/12)²-32,5)
- = -0,12 (x-35/12)² + (1181/240)
Scheitelpunkt (Näherungswerte) : S (2,92/ 4,92)
2,38 (Leo) = y
=-0,2 (x-2,25)² +5,0125
x=5,878 also ca. 5,9
...du weißt ja wie man dann umformt....
Nullstellen: x (1 und 2) = -p/2 +/- (p²/4 -q)
- 0=-0,12x² +0,7 x +3,9
- =x² -35/6 x- 32,5
- p= -35/6
- q=-32,5
- x (negative x nicht entscheidend) = 9,3
- 9,3-5,9=3,4 m hinter Leo, etwa dein Wert
Ich hoffe du kannst das nachvollziehen.

Ist doch gar nicht so schwer. Du bestimmst mit Hilfe der ersten und zweiten Ableitung den Hochpunkt. Und das war's dann schon.
