Mathe - Wie bestimme ich das Unendlichkeitsverhalten richtig mit kleinen und großen Werten einsetzten?
Folgendes Problem:
Eigentlich dachte ich, kann ich nun alles, aber eine Aufgabe hat wie jedes mal alles wieder auf den Kopf gestellt.
Das Unendlichkeitsverhalten zu bestimmen ist schon etwas her, ich kann mich nicht mehr genau erinnern und scheine beim lernen irgendwie was übersehen zu haben.
Beispiel:
f(x) = -0,2x³ + 2x + 1
Nun betrachtet man die Zahl mit dem höchsten Exponent.
-0,2x³. Dann muss man einmnal x--> - oo und einmal x --> +oo bestimmen. Zuerst aber x--> -oo!
Dann habe ich einfach immer irgendwas eingesetzt, z.B. 5 bzw. -5. Hier also:
x --> -oo
-0,2 * (-5)³ = 25 also positiv. D.h., der Graph kommt aus dem positiven also von links oben.
Dann halt das selbe mit
x --> +oo
-0,2 * 5³ = -25 also negativ, d.h, der Graph geht von links oben nach rechts unten.
Jetzt kam aber folgendes: f(x) = 0,1x^4 - 0,5x² + 1
Ich habe es genauso gemacht. Dabei kam raus:
f(x) --> -oo f(x) -->+oo
D.h, der Graph geht von links unten nach rechts oben.
Laut den Lösungen stimmt das aber leider nicht. Der Graph geht dort von links oben nach rechts oben, also müsste es lauten
f(x) --> +oo f(x) -->+oo
Im Internet finde ich die ganze Zeit etwas mit kleinem und großen Wert einsetzten. Ich kann mich fast gar nicht mehr entsinnen, aber das habe ich irgendwie damit schon mal gehört. Allerdings finde ich entweder gar nichts oder nur was mit lim...., was wir sowieso noch nicht hatten.
Kann mir jemand erklären, wie genau man das Unendlichkeitsverhalten jetzt prüft? Was hat es mit den kleinen Werten und großen Werten einsetzten am Hut? Auf meinen Bättern habe ich auch irgendwie jedes mal noch in z.B. x³ eingesetzt und geprüft, danach mit dem Rest also z.B. dann -0,2 * x³. Wenn beim einen immer -, beim anderen + kam, hat aber immer die "ganze Zahl" gewonnen. Ich verstehe das alles nicht wirklich :/
6 Antworten

Du kannst das meistens schon am Grad des Polynoms sehen (ohne das man jetzt den Vorfaktor berücksichtigt).
Gerade: Verläuft für x---> +/- unendlich gegen +unendlich
Ungerade: Verläuft für x----> +unendlich gegen +unendlich
Verläuft für x ----> -unendlich gegen - unendlich
Und zu guter letzt musst du eigentlich nur noch den Vorfaktor berücksichtigen, für einen positiven Wert gelten obige Aussagen. Für einen negativen Wert musst du die Aussagen einfach umkehren. Hier aber noch ein paar Beispiele:
[Dabei sei links: x ---> - unendlich und rechts: x----> +unendlich]
f(x) = x^5 (ungerade)
links: -unendlich
rechts: +unendlich
g(x) = x (ungerade)
links: -unendlich
rechts: +unendlich
h(x) = -x^3 (ungerade)
links: +unendlich
rechts: - unendlich
d(x) = x^2 (gerade)
links: +unendlich
rechts: +unendlich
s(x) = -x^4 (gerade)
links: - unendlich
rechts: - unendlich
Und nun an deinem Beispiel:
f(x) = 0,1x^4 - 0,5x² + 1
Also betrachten wir:
g(x) = 0,1x^4 (positiver Vorfaktor, gerader Exponent)
----> links: +unendlich
----> rechts: +uendlich

Jap, jetzt hab ich es. So ein einfacher dummer Fehler hat mich mal wieder kompett aus dem Konzept gebracht. Ich habe einfach vergessen Klammern zu machen und stattdessen immer die (-) Taste vom Taschenrechner genutzt....
Danke trotzdem vielmals!

Tut mir Leid, keine Ahnung, ich bin so schlecht in Mathe :( Falls dir niemand antwortet, frag doch Eltern oder Geschwister oder Klassenkameraden ob sie dir helfen oder dir die Lösung schicken. Oder gib die Gleivhung oder was das ist in einem guten Taschenrechner ein :)
Jaa.. meine Antwort war unnötig sry <3

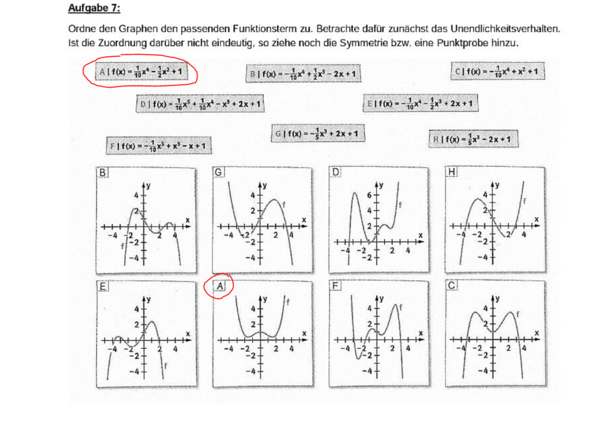
Der GTR bringt mir leider nichts, weil der was komplett anderes ausgibt. Bei A irgendeine Parabel, ganz anders als auf dem Blatt. Das ist bei den anderen, die ich zum Teil auch richtig hatte absolut gleich. Obwohl ich es da richtig habe, gibt der GTR einen ganz anderen Graphen raus. Das ist wohl extra so, damit wir damit nicht einfach ablesen können. Weil die Funktionen ähneln halt nicht mal ansatzweise dem, was auf dem Blatt ist ;) Aber trotzdem danke..

Höchster Exponent gerade, positives Vorzeichen:
x -> -unendlich = +unendlich
x -> +unendlich = +unendlich
Höchster Exponent gerade, negatives Vorzeichen:
x -> -unendlich = -unendlich
x -> +unendlich = -unendlich
Bei einer Potenz mit geradem Exponenten keine negativen Ergebnisse möglich, außer es gibt ein negatives Vorzeichen.
Höchster Exponent ungerade, positives Vorzeichen:
x -> -unendlich = -unendlich
x -> +unendlich = +unendlich
Höchster Exponent ungerade, negatives Vorzeichen:
x -> -unendlich = +unendlich
x -> +unendlich = -unendlich
Negative Ergebnisse bei negativen Werten, positive Ergebnisse bei positiven Werten, negatives Vorzeichen tauscht das dann.

Wenn du einen negativen Wert mit einem ungeraden Exponenten potenzierst, bleibt das Vorzeichen - erhalten. Wenn du jedoch mit einem geraden Exponenten potenziest, fällt das Minus weg.
Hilft dir das weiter?

Leider nicht so wirklich. Ich muss halt wissen, wie man es aufschreibt und wie man das genau prüft. Ich habe ja sowieso nen Taschenrechner.... Wichtig ist für mich einfach, wie ich das nun prüfen kann, wo ich was einsetzten muss und was es mit den kleinen und großen Werten auf sich hat :(

Du hast dein Polynom f(x)=a+bx+cx²+....+z(x^n)
Dann suchst du den höchsten Exponenten, hier also n und betrachtest den dazugehörigen Vorfaktor z.
Wenn z>0 und n gerade gilt f(x)->+oo (für x->+oo oder x->-oo)
Wenn z<0 und n gerade gilt f(x)->-oo (für x->+oo oder x->-oo)
Wenn z>0 und n ungerade gilt f(x)->+oo (für x->+oo) und f(x)->-oo (für x->-oo
Wenn z<0 und n ungerade gilt f(x)->-oo (für x->+oo) und f(x)->+oo (für x->-oo

x ^ 3 = x * x * x
-0.2 * x ^ 3 = -0.2 * (x * x * x)
Wenn ich jetzt folgendes habe:
f(x) = 0,1x^4 und dann negative Werte einsetzten muss, wie genau muss ich einsetzten. Vielleicht lag auch dort mein fehler und der rest war richtig.
Sprich:
0,1* (-5^4) ? Falsch oder?
Ich hatte es so:
0,1 * (-) 5^4
Dieses (-) ist halt die Taste am Taschenrechner.
Oder so:
0,1 * (-5)^4 .
Was ist dabei richtig, denn das verändert das Vorzeichen ja enorm.