Zwei Summen berechnen mit verschiedenen Grenzen ?
Hallo Leute,
ich lerne gerade die Summenzeichen. Aber ich verstehe gar nicht wie man zwei Summen berechnet , deren Grenzen unterschiedlich sind.
Ich habe was berechnet ( siehe Bild)... aber ich bin mir nicht sicher welche Grenzen/Summen man ,,dazu addiert" . Könntet ihr drauf schauen ?
Ich bitte um Hilfe!
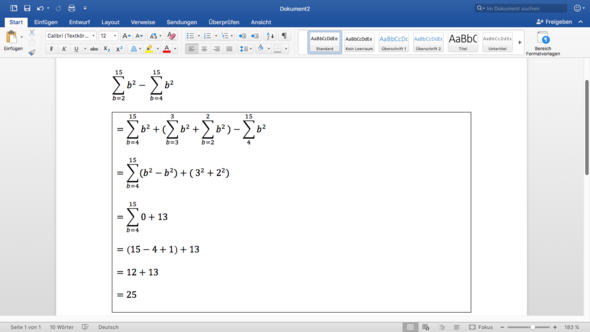
3 Antworten
die erste summe kann aufgeteilt werden in
Summe_k=(2 bis 3) b² + Summe_(k=4 bis 15) b²
Die zweite Summe entfällt dann nach Subtraktion mit sich selbst und es bleibt 2² + 3² über.
Ich versteh auch nicht, was du in dem Schritt machst, in dem du die 0en aufsummierst. Da kommt 0 raus.
0+0+0+0+0....+ 0 = 0 oder?
Danke , für deine Kommentare bei den Beiträgen der anderen zu meiner Frage. Habe das gar nicht gesehen , dass du das warst im anderen Beitrag !
Hallo :) Danke für deine Antwort! Haha ja da sollte eigentlich auch 0 rauskommen Also : 12*0+13= 13 als Endergebnis ? Ich verstehe das Konzept nicht genau warum Summe_k=(2 bis 3) dazu addiert wird und nicht Summe_k=(3 bis 4) ich weiß nicht welche grenzen dazu addiert werden :(
Summe_k=(2 bis 15) b² =
2²+3²+4²+5²+...+15²
Summe_k=(4 bis 15) b² =
4² + 5² + 6² +...+ 15²
Man kanns ja mal so untereinanderschreiben
2²+3²+4²+5²+...+15²
4²+5²+...+15²
Man sieht, dass die zweite Summe in der ersten mit drin ist. Wenn du nun die zweite Summe von der ersten abziehst, bleibt nur noch 2²+3² = 13 über.
Nee für b = 4 bis 15 addierst du immer 0 + 0 + 0 ... und ganz am Ende dann die 13^^
Hallo, danke für deine Antwort!! Also dann: 12*0 + 13 = 13 für b=4 bis 15 ?Könntest du mir vllt. sagen warum man die Summen für b=2 und b=3 ,,dazu addiert" und ist das überhaupt richtig ???? ... und warum nicht Summe für b=4 und b=3 ? Ich verstehe das Konzept nicht ganz welche Summe bzw. Grenze man ,,dazu addiert" ...
also hier ist zum einen die Summe von b=4 bis 15, die am Ende der ersten Zeile aber direkt wieder subtrahiert wird, also hast du da = 0^^ brauchst das also eigentlich nicht weiter zu beachten hier
dann hast du noch die Summe b² für alle b von 3 bis 3 (also für b = 3 einfach) und die Summe b² für alle b von 2 bis 2 (also einfach für b = 2)
du kannst dir das allgemein einfach so vorstellen: die summe von den b²-Termen für alle b´s von 3 bis 15 ist einfach nur = 3² + 4² + ... + 15² , ist halt nur ne andere Schreibweise :) vielleicht geht´s dann leichter
Dankeschön , jetzt kann ich mir es besser vorstellen !!!
Ich habe es jetzt nicht nachgerechnet, aber das Prinzip stimmt bei den Summen. Wenn eine Summe von 2 bis 14 läuft und eine andere von 4 bis 14, dann kannst du die so zusammenfassen, dass zwei von 4 bis 14 laufen.
Dann bleiben natürlich noch zwei Summanden übrig, die extra dargestellt werden müssen, nämlich die Glieder, die zu den Laufindizes 2 und 3 gehören.
Man kann dann so tun, als ob es Summen seien, die von 2 bis 2 bzw. von 3 bis 3 laufen, damit alles wie Summen aussieht. Man hätte diese Glieder auch schon ausgerechnet dazwischen stellen können.
Hallo ich danke dir sehr für die Antwort !!
Also z.B. wenn eine Summe von 4 bis 9 und die andere Summe von 5 bis 10 läuft ... wäre es egal ob ich dann als ,,Hauptindizes" 4 bis 10 oder von 5 bis 9 nehme? ich muss dann nur schauen welche Summanden und deren Laufindizes extra dargestellt werden ? Könntest du mir das vllt. hier für dieses Beispiel auch so erklären wie in deinem ersten Betrag ?
Achso: Also dann geht meine Summe von 5 bis 9 . Und die zwei extra Summanden wären dann die mit den Laufindizes 4 und 10 ? :)
Es geht ja ums Prinzip. Wenn ich nach dem Begucken des Bilds leicht abgelenkt 14 statt 15 geschrieben habe, ändert das ja nichts an der Tatsache. Wenn dann bei der Zusammenfassung bestimmte Glieder nicht erfasst werden, muss man die halt extra schreiben, egal welche es sind.
Und man kann z.b. eine 3 immer in Summenform schreiben als
∑ i von i =3 bis 3.
In deinem Beispiel musst du die gemeinsame Summe von 5 bis 9 laufen lassen. Aus der einen Summe bleibt Summand Nr. 4 übrig, aus der anderen Summand Nr. 10.
:) Dankeschön !!! Ich hätte nur noch eine Frage:
Aufgabe: Summe_b=(4 bis 9 ) ( c^3) - Summe_b=(5 bis 10)(c^3)
Rechnungsansatz (RA):
1.)Summe_b=(5 bis 9)(c^3) + (4^3) - Summe_b=(5 bis 9)(c^3)+ (10^3)
oder
2.) Summe_b=(5 bis 9)(c^3) +(4^3) - ( Summe_b=(5 bis 9)(c^3)+ (10^3))
Frage:
bei RA 1.) dann addiere ich die übrigen Summanden mit dem plus .
bei RA 2.) Da habe ich den letzten Teil in Klammern gesetzt aber dadurch würde später verschiedene Vorzeichen als bei RA 1.) rauskommen , dann hätte man ,,-10^3" und bei RA 1.) dann ,,+10^3)
Aus der einen Summe bleibt Summand nr.4 übrig aus der anderen Summand nr.10 ... müsse ich dann die Summanden zu ihrer zugehörigen Summe addieren oder kann ich die einfach am ende dazu addieren ( positiv, plus) ?
Boah, das überblicke ich zu diesem Zeitpunkt auch nicht mehr so richtig. Ich kann es mir ja morgen nochmal ansehen.
Das Prinzip ist jedenfalls klar; und so oft kommt es nicht vor, außer wenn ein Schulbuch einige Übungsaufgaben gebastelt hat.
Also Frage: wir haben Summe a + Summe b. Bei Summe a bleibt Summand nr.4 übrig und bei Summe b Summand nr.10. kann ich z.B. den Summand nr. 4( der gehört ja zu Summe a) anstatt bei Summe a bei Summe b addieren oder muss der bei summe a bleiben, weil der zu dem ,,gehört" ?
Tut mir echt leid ! Ich danke dir aber so sehr für die mühen und ich habe endlich das Prinzip verstanden :)
Der zweite Ansatz ist der richtige, da das Minus vor der Summe_(c=5 bis 10) c³ steht und wenn du den Summanden mit index 10 da rausholst, hast du an der Summe an sich nichts geändert. Das Minus muss auch vor dem 10³ stehen. Sprich: Die Klammer gehört dahin. Das macht auch Sinn weil
Summe_(c=4 bis 9) c³ - Summe_(c=5 bis 10) c³=
4³+5³+...+9³ - (5³ + 6³ +... + 10³) =
4³ + 5³+ 6³ + 7³ + 8³+ 9³ - 5³ - 6³ - 7³ - 8³ - 9³-10³ = 4³ -10³
Summe a + Summe b
Weder - noch.
Ein freier Summand gehört nicht zu einer Summe.
Wenn du eine völlig neue Summe von zwei Termen unter einem Laufindex gebildet hast, sind die herausgenommenen Glieder außen vor. Entweder sind sie jetzt nur noch einzelne Summanden oder es gelingt, sie unter einem anderen Laufindex zusammenzubringen.
Diese kurze Auskunft schaffe ich gerade noch mit müden Augen.
Ja du kannst den summand den du aus der Summe A geholt hast auch in die summe aus B packen, sofern diese sich eben durch die Summenvorschrift c³ darstellen lässt ( tut es hier ja).
Jetzt habe ich alles verstanden !!! Ich danke dir so sehr !!! :) Ich wünsche dir noch ne gute Nacht !
Ich meinte natürlich Summe_b= ... und nicht k.