Kovarianz berechnen, wie ist diese Formel zu interpretieren? Und ist das für stetige oder diskrete Zufallsvariablen?
Kovarianzfolie:

Was mir hier unklar ist, für was ist dieses g(x,y)? Das ist doch das gleiche wie wenn man einen bestimmten Wert für X und Y hat und soll damit dieses E(X-\mu_x)(Y-\mu_y) ersetzen oder? Und fehlt hier:
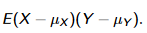
Nicht noch eine Klammer sollte es nicht sein:
E((X-mu_x)(Y-mu_y)) ?
Und wann nutzt man dieses g(x,y), hier im Beispiel hat man diese VErschiebungsregel genutzt:


Wann nutzt man g(x,y)? WEil nach der Verschiebungsregel, kann man diese Regel:
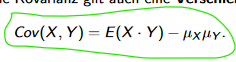
immer nutzen? Ist dann g(x,y) nicht überflüssig?
Und welche Art von Zufallsvariablen haben wir hier? Das wurde nicht erwähnt, sind es stetige, diskrete? Weil später werden auch Grenzwärtsetze eingeführt, da stehen auch keine Bezeichnungen für die Zufallsvariabln?
Da haben wir z. B. Satz von Bernoulli stehen, was ja eig. für diskrete Zufalslvariablen wäre?
2 Antworten
Was mir hier unklar ist, für was ist dieses g(x,y)?
Vermutlich die Funktion dessen Erwartungswert bestimmt werden soll, um den Erwartungswert zu bestimmen.
Nicht noch eine Klammer sollte es nicht sein:
Formal: ja.
Ist dann g(x,y) nicht überflüssig?
Nein. Denn erstens ist das für die Definition von der Covarianz wichtig, und zweitens ist das für theoretische Betrachtungen wichtig.
Und welche Art von Zufallsvariablen haben wir hier? Das wurde nicht erwähnt, sind es stetige, diskrete?
Wenn die nicht spezifiziert werden, sind beliebige gemeint.
Was dieses g(x,y) hier soll, weiss ich auch nicht so recht. Vielleicht will man die Kovarianz als E(g(X,Y)) darstellen, ich wüsste aber nicht wozu.
Auch die Notation sigma_{X,Y} erschliesst sich mir nicht, denn wenn X = Y, dann steht sigma_{X,X} für die Varianz von X, obwohl "sigma" üblicherweise für die Standardabweichung reserviert ist.