Konvergiert diese Mittelwertfolge?
Ich soll entweder zeigen oder widerlegen ob diese Mittelwertfolge konvergiert.
Bin aber etwas planlos… zeigen würde ich das wenn mit dem Epsilon Kriterium…
Wenn $(x_k){k\geq 1} \in S(\mathbb{R})$ konvergiert. Dann konvertiert auch $\left(\frac{1}{n}\sum_{k=1}^{n}x_k\right)_{n\geq 1}$.
3 Antworten

Wenn n gegen Unendlich geht, dann erhalten wir eine Reihe beginnend bei k = 1.
Wir betrachten die Partialsummen. Da x_k konvergiert, ist die Folge beschränkt, also existiert ein reelles C mit
|x_k| < C
und daraus folgt, dass die absolute Summe von k = 1 bis n, also
1/n * sum{k=1}{n}{ | x_k | } < 1/n * sum{k=1}{n}{ C } = 1/n * (n * C) = C,
ebenfalls beschränkt ist.
Da es für alle n gilt, ist diese Reihe, also der Mittelwert für n gegen Unendlich, (absolut) konvergent.
Hier nochmal formal:
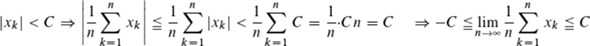
|x_k| < C \imp \left|\frac{ 1 }{ n }\Sum{ k=1 }{ n }{ x_k}\right|\leq \frac{1}{n}\sum_{k=1}^{n}|x_k| < \frac{ 1 }{ n }\Sum{ k=1 }{n }{ C } = \frac{ 1 }{ n }*Cn=C \quad \imp -C\leq \nlimes{ \frac{ 1 }{ n }\Sum{ k=1 }{ n }{ x_k } }\leq C
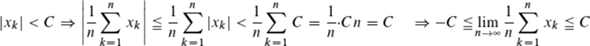

Natürlich. Wenn es eine Nullfolge ist, sind - nach Definition des Grenzwertes - ab einem bestimmten Index alle Folgenglieder kleiner als jede positive reelle Zahl.
Wir können also zum Beispiel für C = 1/2 ein K finden, sodass alle x_k mit k ≥ K betraglich kleiner als 1/2 sind.
C kann ja beliebig groß gewhält sein. Der Betrag der Folgenglieder muss einfach nur kleiner sein.

Ich trage eben noch dieses Beispiel zu meinem vorherigen Kommentar nach.
Die wohl bekannteste Nullfolge ist die harmonische Folge (1/n).
Sie ist beispielsweise durch Zwei beschränkt, denn
|1/n| < 2 (für alle ganzen n≠0).
Der Grenzwert 0 ist natürlich dann auch kleiner als Zwei.

Ich denke, du hast nur Beschränktheit nachgewiesen, nicht Konvergenz

Doch, für die Mittelwertsumme habe ich auch die Konvergenz nachgewiesen.
Denn die Reihe über |x_k| ist monoton steigend und durch C beschränkt. Somit ist sie konvergent (Monotoniekriterium für Reihen)


Aber für x_k gilt es dann auch.
(Jede abslolut konvergente Reihe ich auch bedingt konvergent)



Ist doch konvergent.
Mit dem Quotientkriterium würden wir keine Aussage erhalten (weil der Grenzwert gleich Eins ist).
Aber die Folge (x_k) ist mit Zwei beschränkt. So können wir abschätzen.
1/n * sum(k=1; n)( |x_k| ) < 1/n * sum(k=1; n)( 2 ) = 1/n * 2n = 2.
Das gilt dann auch für den Grenzwert, da es für alle natürlichen n gilt.
Die Reihe über |x_k| ist also konvergent (Monotoniekriterium für Reihen). Somit ist die Reihe über x_k auch konvergent (jede absolut konvergente Reihe ist auch bedingt konvergent).
Nach Wolfram|Alpha hat sie den Reihenwert Eins.

Vergiss den Link, habe dort einen Fehler gemacht. Hier
https://www.wolframalpha.com/input?i=1%2Fn+*+sum%28k%3D1+to+n%29%281%2B%28%E2%80%931%29%5Ek%2Fk%29
sieht man gut die Asymptote bei der horizontalen Eins.

"Denn die Reihe über |x_k| ist monoton steigend und durch C beschränkt." hast du geschrieben. Dazu wollte ich mit x_k = 1 + (-1)^n / n ein Gegenbeispiel geben.

Ich habe x_k = 1 + (–1)^n / n gesetzt.
Siehe hier. Dort sieht man gut die Konvergenz (und ich habe nicht |x_k| oder was anderes eingetragen).

Vielleicht irritierd es dich, dass die Reihe mit x_k konvergiert, wenn sie mit |x_k| konvergiert.
Wenn eine Reihe über |x_k| konvergent ist, kann du die Partialsummen betrachten, wobei du (bei reellen x_k) die Summe S zu zwei Summen S+ und S– aufspaltest.
Bei S+ sind alle Summanden mit nichtnegativem Vorzeichen, bei S– jene mit negativem Vorzeichen.
S+ ist konvgent, da S konvergent ist (also die Reihe über |x_k|).
Das selbe für S–, da dort –1 ausgeklammert werden kann. Die Summe selbst enthält dann auch nur noch nichtnegative Summanden. Sie konvergiert also auch, da S konvergiert.
S ist also zu beiden eine konvergente Majorante (das –1 bei S– brauchen wir nicht beachten, da der Reihenwert dadurch nur ein anderes Vorzeichen hat). Nach dem Majorantenkriterium sind S+ und S– also konvergent.
Und nach den Rechengesetzen für Reihen/Folgen, muss auch (S+) + (S–) konvergent sein. Also die Reihe über x_k.
Ansonsten weiß ich nicht, wie ich weiterhelfen kann.

Wir reden aneinander vorbei.
Du hast geschrieben: "Denn die Reihe über |x_k| ist monoton steigend und durch C beschränkt. Somit ist sie konvergent (Monotoniekriterium für Reihen)"
Mit der Folge x_n = 1 + (-1)^n / n wollte ich zeigen, dass diese Argumentation nicht stimmen kann.
Dass diese Folge und die "Mittelwertfolge" konvergieren ist unbestritten. Aber ich kann deine Begründung dafür nicht nachvollziehen.
Denn weder x_k, noch |x_k|, noch die Mittelwertfolge sind monoton wachsend. Beispiel:
x_18 = 1.056, Mittelwert bis dahin = 0.9630
x_19 = 0.947, Mittelwert bis dahin = 0.9622

Es ist natürlich korrekt, dass die Reihe über x_k nicht monoton sein muss, aber die über |x_k,| bleibt es doch immer noch.
Sie ist immer monoton steigend, da sie nicht streng monoton fallend sein kann (gibt ja wegen dem Betrag keine negativen Vorzeichen).
Die Folge |1 + (–1)^k / k| selbst ist nicht monoton steigend. Aber die Reihe über diese. Und das Monotoniekreiterium gilt ja für die Reihe (wie bei Folgen auch, da die Reihe ja ein Sonderfall einer Folge ist).

Warum redest du eigentlich die ganze Zeit von "Reihe"? Es geht hier nicht um Reihen. Vielleicht ist da des Pudels Kern unseres Missverständnisses.

Es geht um die Folge (1/n * sum(k=1; n)( x_k )) und ihre Konvergenz.
Wenn wir den Faktor 1/n in die Summe reinziehen und n gegen Unendlich gehen lassen, erhalten wir eine Reihe (eine Reihe ist eine Folge von Summen). Also passt das doch(?).
Aber undabhängig davon, war mein Weg doch eigentlich klar, oder?

Das ist keine Reihe, da die Summanden ja bei jedem Schritt verändert werden. Eine Reihe ist einen Folge von Partialsummen, bei dir wird in jedem Schritt (n --> n+1) alles neu "durchgemischt".

Wieso wird es neu "durchmischt"?
zu x_1+x_2+...x_n kommt immer ein x_(n+1) hinzu.
Wahrscheinlich meinst du es wegen dem Vorfaktor 1/n, der sich jedes mal ändert.
Da bin ich mir gerade ehrlich gesagt nicht sicher, inwiefern der Begriff der Reihe passt. Dann sage ich nun einfach Folge dazu.
Dass die Folge konvergiert mit dem oben beschriebenen Weg (siehe Antwort) ist aber weiterhin korrekt.
Das Monotoniekriterium gilt ja für Folgen. Die Folge ist also durch C beschränkt.
Da wir nicht von absoluter "Reiher" sprechnen können, teilen wir die Folge in zwei Teilfolgen, wobei die x_k in der jeweiligen Folge das selbe Vorzeichen haben.
Für diese beiden Teilfolgen gilt dann das Monotoniekriterium. Somit ist die (Ausgangs-)Folge auch konvergent, nach den Rechengesetzen für Reihen.

Zerlege die Summe
( x(1) + .... + x(n) ) / n in zwei Teile, einmal bis N, einmal ab N+1,
( x(1) + .... + x(N) ) / n + ( x(N+1) + .... + x(n) ) / n,
zu N kommen wir gleich.
Der Grenzwert der Folge (und unser Kandidat für die Mittelwertfolge) sei a, dann gibt es zu gegebenem epsilon ein N, so dass
| a - x(k) | < epsilon/2 für k > N.
Ausserdem gibt es zu epsilon und N ein N2 > N, so dass
| ( (x(1)-a) + .... + (x(N)-a) ) / n | < epsilon/2 für n > N2.
Damit hat man für n > N2
| ( x(1) + .... + x(n) ) / n - a |
= | ( x(1) + .... + x(N) ) / n + ( x(N+1) + .... + x(n) ) / n - a |
= | ( (x(1)-a) + .... + (x(N)-a) ) / n + ( (x(N+1)-a) + .... + (x(n)-a) ) / n |
< epsilon/2 + epsilon/2 * (N+2-n)/n
< epsilon

Konvergiert diese Mittelwertfolge?
Ja, diese Folge konvergiert.
Den Part verstehe ich noch nicht.
“Wir betrachten die Partialsummen. Da x_k konvergiert, ist die Folge beschränkt, also existiert ein reelles C mit
|x_k| < C“
Was ist wenn die Folge gehen null konvergiert. Gibt es dann immer noch ein C was größer als die Folge ist?