Funktionen und ihre Eigenschaften ?
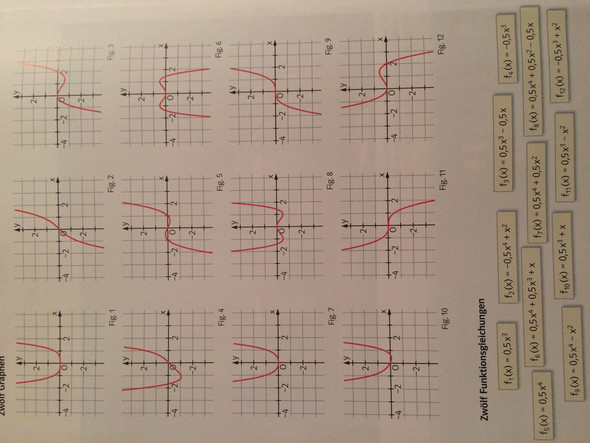
Heyyy Leute, ich muss 12 Funktionen zu 12 Graphen zuordnen, jedoch weiß ich nicht welche Funktion zu welchem Graph gehört. Könnte mir das jemand erklären?
3 Antworten
Alle Polynome haben kein Offset, also gehen sie alle durch 0-Punkt.
Polynome mit nur geraden Potenzen gehen beide Enden in die Richtung des Faktors der höchsten Potenz...
Nur Fig6 hat negative Enden und nur f2 hat negativen Faktor!
Fig6 - f2
Fig8 ist dazu negiert und symmetrisch:
Fig8 - f9
...
Das könnte ich in vielen Sätzen mit den anderen f... so weitermachen...
aber ich bin für effektive Wege und mache das mit dem universellen Liniendiagramm:
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
f(x): aA[iFarb]*pow(x,4)+aB[iFarb]*pow(x,3)+aC[iFarb]*pow(x,2)+aD[iFarb]*x
da Arrays bei 0 beginnen, wird aus 1...12 nun 0...11:
Feld aA für Faktoren der 4er Potenzen:
aA=Array(0,-0.5,0,0,0.5,0.5,0.5,0.5,0.5,0,0,0);
aB für Faktoren der 3er Potenzen:
aB=Array(0.5,0,0.5,-0.5,0,0.5,0,0,0,0.5,0.5,-0.5);
2er
aC=Array(0,1,0,0,0,0,0.5,0.5,-1,0,-1,1);
aD=Array(0,0,-0.5,0,0,1,0,-0.5,0,1,0,0);
Init: aA=Array(0,-0.5,0,0,0.5,0.5,0.5,0.5,0.5,0,0,0);aB=Array(0.5,0,0.5,-0.5,0,0.5,0,0,0,0.5,0.5,-0.5);aC=Array(0,1,0,0,0,0,0.5,0.5,-1,0,-1,1);aD=Array(0,0,-0.5,0,0,1,0,-0.5,0,1,0,0);
iFarb ist Index der Kurve, die je 1 Farbe zugewiesen bekommt
siehe Bild im Anhang
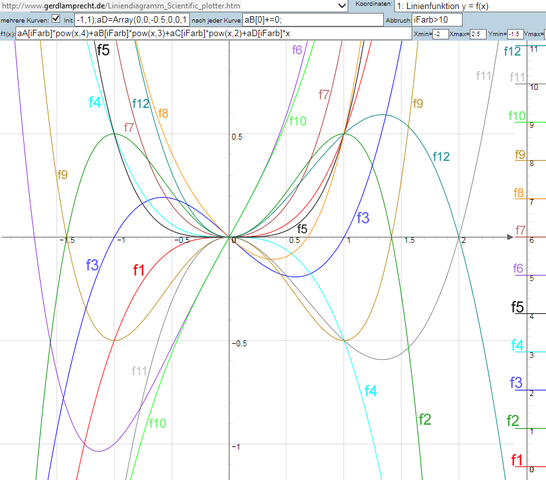
Fig. 9 sieht man auf den 1. Blick, dass es die k*x³ Funktion f1 ist:
Fig9 - f1
Fig2 ist nun einfach um x nach oben verschoben, also f10
(sie wird damit steiler: 2 ungerade Potenzen ergänzen sich)
Fig2 - f10
Fig 5 ist die Verstärkung genau negiert, also f3...
Fig5 - f3
Über bleibt bei den x³ mit positiven k Fig3 , also f11. Hier bewirkt die geradzahlige Potenz mit negativen Faktor bei negativen x ein Verstärken des Anstieges, und bei kleinen positiven x-Werten eine entgegengesetzte Kraft, die es bis x=2 schafft, gegen den Anstieg gegenzuarbeiten -> aber bei größer werdenden x den Kampf verliert und bei noch größeren x so stark verliert, dass man es fast weglassen kann:
Fig3 - f11
Will dir jz nicht die Aufgabe lösen :) , aber du musst die Funktion für jeweils x=0 und x=1 lösen (geht auch mit andren Werten, so ist es aber am einfachsten) , dann kucken in welchen der Graph die Punkte an der ausgerechneten Stelle liegen ( zur Sicherheit kannst du natürlich auch mit bzw. 4 Werten ausprobieren, damit du ganz sicher sein kannst)
Stimmt beides, darum würde ich dir wirklich empfelen Geogebra etc. zu downloaden. Dort wird der ganze Graph angezeigt :)
Wie würde es denn aussehen wenn ich 1 oder 0 einsetze? ☺️
Bzw. bei f(x1) = 0,5 *x^3:
x1 = 0 :
f(x) = 0,5 * 0
f(x) = 0
x2 = 1 :
f(x) = 0,5 * 1^3
f(x) = 0,5
Mir fällt gerade auf das das viele Potenzfunktionen sind darum (Sicherheitshalber) mehr Proben
x3 = 2:
f(x) = 0,5 * 2^3
f(x) = 0,5 * 8
f(x) = 4
Nach "Nachkucken" ist f(x1) = Abbildung 1 ; Ist ein bissel schlecht nachgestellt die Fig. 1-12 , hol dir deshalb ein Programm ,das Funktionen nachstellen kann (bsw. ich benutzte Geogebra). Du siehst auf der Kopie nicht, ob x=2 in Fig. 1 wirklich den Funktionswert 4 besitzt.
Ich mach mal eine weitere Antwort.
Bei f_4 = -0,5 x^3 bekommst du für x = 1 y= -0,5 heraus
Das trifft auf Fig. 3 und 11 zu
entweder machst du jetzt eine zweite Probe (x=0 in beiden Fällen y = 0 ... was dich auch nicht weiter bringt), oder du erkennst, dass Fig.3 nicht punktsymm. ist und deswegen noch ein weiteres x^a in der Gleichung auftauchen muss.
Somit kann nur noch Fig 11 auf f_4 hinhauen ;)
Wie ich geschrieben habe ist 11 Punktsymm. ;)
bei 12) spiegelst du den linken Ast einfach mal an der x und der y Achse und wirst feststellen, dass der nicht genauso aussieht/verläuft wie der rechte Ast
Allgemeint ist die Punktsymmetrie definiert als
f(x) = -f(-x)
Leider setzt das ganze verfahren etwas Vorstellungskraft vorraus :(
Aber woher weiß ich das Figur 3 nicht punktsymmetrisch ist?
Weil die Funktion (einfach erklärt) nicht am Koordinatenursprung (Das Achsenkreuz) verkehrtherum gespiegelt ist
Die Punktsymmetrischen Fig. sind:
2, 5, 9, 11
Punktsymmetrisch heißt im übrigen auch, dass in der Funktion nur x^a mit a = ungerade (also 1, 3, 5, ...) vorkommen darf
Ja man kann sie leider nicht richtig nachsehen, weil die Graphen nicht so groß sind und ich glaube das bei einem ungeraden exponenten der Graph punktsymmetrisch ist und bei einem geraden exponenten achsensymmetrisch ist