Wie beweist man Induktions Anfang (Vollständige Induktion)?
Habe Schwierigkeiten bei Induktions Anfang.
Wenn ich bei Aufgabenteil (a) n=0 setze kommt da 0 raus. Wenn ich für k=0 setze kommt da 1/0 raus was unendlich ist.
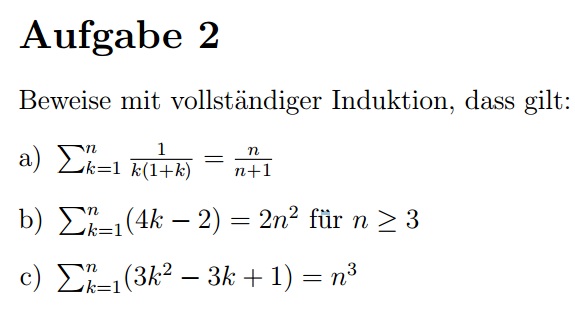
3 Antworten
Du wählst beim Induktionsanfang das erst beste n aus und zeigt, dass genau für dieses n die Annahme gilt. In Aufgabe a wäre das n = 1, da der Summationsindex k 1 ist
Btw: Zahl/0 ist nicht definiert und nicht etwa unendlich, deswegen starte die Summe ja bei 1.
In Aufgabe b hast du den Zusatz, dass die Annahme für alle n >= 3 gilt. Hier wählst du n = 3 für den Anfang. Bei c analog wie bei a
Warum willst du für n Null setzen? Setze n=1 !
Du könntest auch n = 7 setzen und das als Induktionsanfang nehmen. Dann musst du die Fälle 1 bis 6 anders (durch ausrechnen) zeigen.
Du setzt aber niemals k=0, die Summe beginnt bei k=1