

h(t) = Starthöhe - gefallene Strecke in Abhängigkeit zur Zeit.
h(t) = 100m - s(t)
h(t) = 100m - 4,9t^2


h(t) = Starthöhe - gefallene Strecke in Abhängigkeit zur Zeit.
h(t) = 100m - s(t)
h(t) = 100m - 4,9t^2


Also so wie ich das verstehe, ist die Zusatzgeschwindigkeit ja die Geschwindigkeitsänderung in einem Intervall von t1 bis t2. Während der Ball steigt, wird ja die kinetische Energie des Balls in potentielle Energie umgewandelt, da er an Höhe gewinnt. D.h seine Geschwindigkeit fällt zwischen 1 und 6 stetig, bis sie bei 6 ihren Tiefpunkt erreicht, das sieht man daran, dass die Steigung der Tangente bei 6 = 0m/s ist (Waagerechte Tangente). Ich würde also einfach die Tangentensteigung bei 1 ablesen. Dann die Tangentensteigung bei 6. Zusatzgeschwindigkeit = Geschwindigkeit bei 6 - Geschwindigkeit bei 1. Die Zusatzgeschwindigkeit wird damit negativ sein, da der Ball ja zwischen 1 und 6 an Geschwindigkeit verliert.
Gibt aber keine Garantie, dass das richtig ist, ich hoffe, dass das hilfreich ist. (:


Man darf für x alle reelen Zahlen außer 0 einsetzen, somit ist der Definitionsbereich alle reelen Zahlen außer Null. a darf außerdem auch nicht Null sein, darf aber ansonst auch eine beliebige reele Zahl sein.
für x -> 0 x < 0 f(x) -> - ∞
für x -> 0 x > 0 f(x)= -> ∞

Grafik wurde erstellt mit: https://www.geogebra.org/graphing?lang=de


Du musst mit -1 multiplizieren, dann hast du: 25/a^2 = 1 und kannst ganz normal weiter auflösen. Als Ergebnisse kommen +5 und -5 raus.


Nein das ist falsch. Geraden haben die allgemeine Geradengleichung y = mx + c.
Die Geraden haben unterschiedliche Steigungen, somit ist das m anders. Die y-Achsenabschnitte sind aber richtig.
a) y = 2x + 3
b) y = 0.5x - 3


Ich hätte gesagt 74cm - 13cm = 61cm


Zunächst einmal muss ich sagen, dass es keine Garantie gibt, dass das richtig ist. Aber das sind meine Lösungen:
Eigentlich müsste man erst die -30 Grad in Kelvin umrechnen, und dann 80 Grad, und dann die Temperaturdifferenz in K angeben, daher, dass es eine Differenz ist, ist das aber egal.
Ich hoffe das hilft! (:
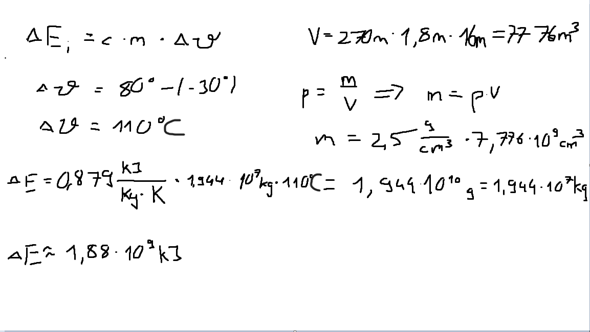

Quelle für die Wärmedehnzahl von Beton:
https://www.beton.wiki/index.php?title=W%C3%A4rmedehnzahl


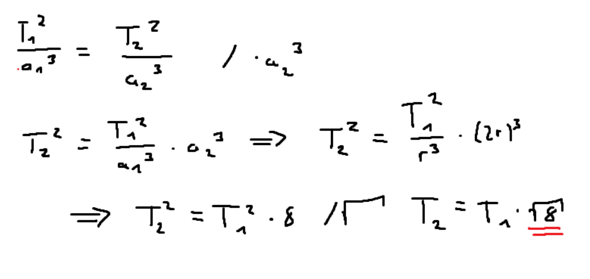
Die Wurzel 8 kommt daher, dass man (2r)^3 macht


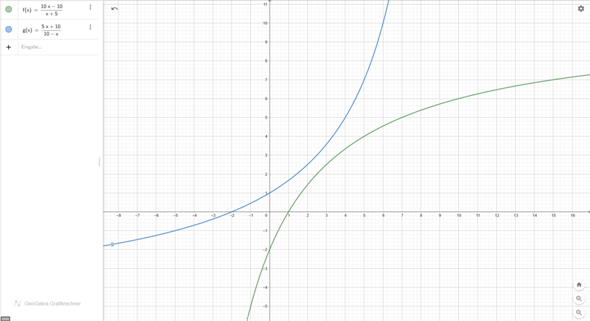
Du musst klever ausklammern, um die Aufgabe lösen zu können. Dein Ansatz war schon richtig:
f(x) = (10x - 10) / (x + 5)
y = (10x - 10) / (x + 5) / * (x + 5)
y * (x + 5) = 10x - 10
yx + 5y = 10x - 10 / + 10
yx + 5y + 10 = 10x / - yx
5y + 10 = 10x - yx
5y + 10 = x * (10 - y) / (10 - y)
(5y + 10) / (10 - y) = x
=> y = (5x + 10) / (10 - x)


Ich hätte gesagt, dass die Leistung und die Vogelmasse nicht proportional zueinander sind, sondern quadratisch voneinander abhängen, da m im Quadrat steht. daher, dass im Bruch nur konstante Werte sind, sprich die Luftdichte p, S und die konstante Geschwindigkeit v, ist das also letztendlich einfach ein Faktor, der vor m^2 steht. Bspw. wiegt Vogel A doppelt soviel wie Vogel B. D.h Vogel A muss die vierfache Leistung erbringen, wie Vogel B. Der Graph müsste also glaube ich quadratisch und nicht linear sein.
Jetzt noch zu b). Da ist ja die minimale Leistung in Abhängigkeit zur Geschwindigkeit gesucht, sprich ein Tiefpunkt von der Funktion. Du musst also die Funktion nach v Ableiten, und dann Null setzen, dann mit der zweiten Ableitung überprüfen, ob es sich um einen Tiefpunkt handelt.
Bin mir aber wie gesagt nicht 100% sicher, ob meine Antworten stimmen.


-6*(x - 2)^2 = -6 * (x^2 - 4x + 4) = -6x^2 +24x - 24


Bin mir nicht 100 % sicher, aber mein Ansatz ist der folgende: Zunächst weiß man ja, dass die Stromstärke und die Zeit proportional zu der Kupfermenge sind. Somit wäre die Masse m = t * I * p. p ist hierbei ein Proportionalitätsfaktor. Wenn man diesen ausrechnet also 0.12g = 900s * 0.4A * p kommt man für p auf 1/3000 g/As. Daher, dass man nun den Proportionalitätsfaktor hat, kann man jetzt die Formel nach der Zeit umformen. m = t * I * p -> t = m / (I * p) = 0.24g / (1A * 1/3000g/As) = 720s.


Ich habe etwa 96,59cm raus.
Rechenweg: sin(15) = 25cm / c
--> c = 25cm / sin(15) = 96,59cm


Vieles stimmt, aber Fische sind wechselwarm somit müssten Forellen und Thunfische in der anderen Spalte stehen. Wüstenmäuse und Kolibris sind außerdem nicht wechselwarm sondern gleichwarm. (:


Daher, dass es keine Beschriftung der X-Achse gibt kann ich es nicht zu 100% sagen, sieht aber so aus wie f(x)=0.5 sin(x)-0.5


1)
f(x)=(x+4) (x+1) (x-2)
2)
f(x)=(x+3)*x*(x-3)^2
3)
f(x)= -x * (x+4)^2


Du musst gar nicht weiter vorgehen die Gleichung hat einfach keine Lösung. Es gibt keine reele Zahl, die quadriert -20 ergibt, bzw wenn du die Wurzel ziehst steht unter der Wurzel was negatives und somit gibt es keine Lösung (mal abgesehen von den komplexen Zahlen)


Ich glaube du sollst hier eher skizzieren anstatt genau zu zeichnen. Du kannst dir zu nutze machen, dass der höchste Exponent pro Ableitung immer um 1 kleiner wird. Z.b bei dem ersten Beispiel weißt du, dass die Steigung konstant größer wird. Beziehe wichtige Punkte wie Nullstellen, Wendestellen und Extremstellen in die Skizze mit ein. Bspw. bei dem ersten Beispiel ist die erste Ableitung eine lineare Funktion, d.h x^1, die zweite Ablietung einfach nur noch eine Konstante. Dementsprechend handelt es sich bei der zweiten Ableitung wahrscheinlich um eine Parabel.
Ich hoffe das hilft. Wenn nicht, stelle ruhig noch mal eine Nachfrage.


Nun ich kann es dir auch nicht genau beantworten, wieso es so ist. Meine persönliche Erklärung ist, dass in Zeiten der Unsicherheit, wie z.B in der jetzigen Zeit die politischen Flanken, d.h rechts und links immer dazugewinnen. Das war schon immer so. Somit gibt es auch eine zunehmende Sympatisierung für bestimmte Diktatoren, da einfach mehr Menschen rechts- bzw. linksextrem sind. Aber wie gesagt ist das nur meine eigene Meinung und Erklärung.


1) innovative, astonishing
2) secure
3) ich weiß nicht ganz genau, was das Bild zeigen soll
4) fast, reliable
5) cheap, comfortable
6) yummy, easy (to make), delicious
Anmerkung: Ich weiß nicht ganz genau, ob es bei Bild 2) um die App oder das iPad geht.