Zahlenschloss knacken - Kombinatorik?
Hallo, ich habe eine Statistik Aufgabe, wo ich nicht weiß, wie ich sie lösen kann:
- 6- stelliges Zahlenschloss
- man weiß, dass die Ziffern 1, 1, 4, 4, 4 und 8 vorkommen
Frage: wie viele Versuche sind höchstens notwendig, um das Schloss zu knacken.
Vielen Dank im Voraus
5 Antworten

Hallo,
es gibt 6!=720 Möglichkeiten, sechs Elemente in einer Reihe anzuordnen.
Du hast sechs Elemente, von denen allerdings die beiden Einsen und die drei Vieren ununterscheidbar sind.
Du teilst die 720 daher durch (2!*3!)=12 und kommst so auf 60 unterschiedliche Reihenfolgen und somit auf höchstens 60 Versuche.
Herzliche Grüße,
Willy



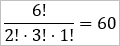
Erklärung dazu:
Wie viele verschiedene Möglichkeiten gibt es die Ziffern 1, 1, 4, 4, 4, 8 anzuordnen?
Es gibt 6! Möglichkeiten 6 verschiedene Elemente in einer Reihe anzuordnen. Nun hat man jedoch 2-mal die gleiche Ziffer 1, weshalb man 2! rausteilen muss. Man hat 3-mal die gleiche Ziffer 4, weshalb man 3! rausteilen muss.
Es gibt demnach 60 verschiedene Kombinationen, weshalb höchstens 60 Versuche notwendig sind, umd das Schloss zu knacken.
Die 60 möglichen Kombinationen sind übrigens:
114448
114484
114844
118444
141448
141484
141844
144148
144184
144418
144481
144814
144841
148144
148414
148441
181444
184144
184414
184441
411448
411484
411844
414148
414184
414418
414481
414814
414841
418144
418414
418441
441148
441184
441418
441481
441814
441841
444118
444181
444811
448114
448141
448411
481144
481414
481441
484114
484141
484411
811444
814144
814414
814441
841144
841414
841441
844114
844141
844411
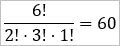

Urnenmodell würde ich versuchen.

Du musst einfach nur berechnen, wie viele verschiedene Möglichkeiten es gibt die Ziffern 1, 1, 4, 4, 4 und 8 anzuordnen. Es handelt sich hier um 3 verschiedene Ziffern, die Reihenfolge der 1en und 4en spielt keine Rolle.
Ich würde erstmal mit der 8 beginnen. Es gibt hierfür 6 mögliche Positionen. Das heißt, dass wir alle nachfolgenden möglichen Anordnungen der 4en und 1en einfach mit 6 multiplizieren.
Für 4en gibt es dann nur noch 5 mögliche Positionen. Wir müssen also jeder 4 eine aus 5 möglichen Positionen zuordnen. Im Urnenmodell wäre dies 3-maliges Ziehen ohne Zurücklegen ohne Beachtung der Reihenfolge (Kombination ohne Wiederholung) => Die Anzahl ergibt sich durch den Binomialkoeffizienten (N über n), mit N = 5 und n = 3.
(5 über 3) = 5! / (3! *(5-3)!) = 5! / (3!*2!) = 1*2*3*4*5/(1*2*3*1*2) = 4*5/(1*2) = 20/2 = 10.
Es gibt also 10 mögliche Positionen für die 4en.
Für die 1en bleiben dann noch 2 mögliche Positionen. Analog folgt (2 über 2) = 2!/2! = 1.
Insgesamt haben wir dann also 6*10*1 = 60 mögliche Anordnungen und dies ist auch die maximale Anzahl an Versuchen.
Das wäre die etwas ausführliche, dafür aber vielleicht anschaulichere, Ausführung. Ansonst verweise ich auf die Antwort von Willy1729. Mit der von ihm genannten Formel lässt sich so was natürlich deutlich schneller rechnen.

6!/(3! * 2!)=60

Danke schonmal. Das Ergebnis hatte ich schon, aber ich weiß den Lösungsweg eben nicht. Hätte ich besser formulieren sollen. Wie kommst du auf diese Formel? Zumindest auf den Teil unterm Bruchstrich?

Das ist Kombinatorik. Du hast 6 Elemente, die du miteinander kombinieren willst. Das ist 6!. Von diesen 6 Elementen sind 3 4er, Daher rührt die 3! im Nenner. Weiterhin hast du 2 1-er, daher die 2! im Nenner.