Sinus durch Grundrechenarten erhalten?
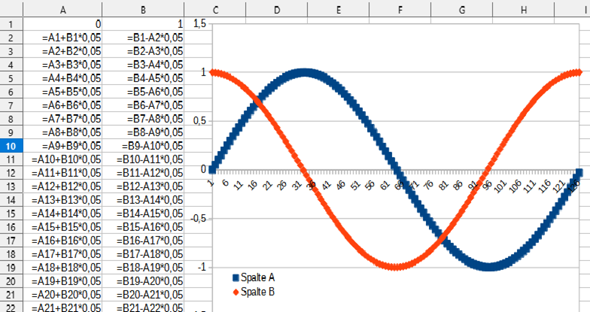
Beim Experimentieren mit einer Tabelle erhielt ich (scheinbar?) diese schöne Sinus-und Cosinusfunktion, ohne die trigonometrischen Funktionen zu nutzen.
Die Funktionsgraphen scheinen wirklich deckungsgleich zu sein.
Irgendwie hat das auch einen Sinn, wenn ich mir die Ableitungen ansehe, aber ich dachte nicht, dass das so einfach geht.
- Kann man das irgendwie sinnvoll rechentechnisch nutzen (z.B. zur Ermittlung der Sinus-Funktionswerte)
- Wenn ich die beiden Spalten als eine Spalte von komplexen Zahlen ansehe, gäbe es eine einfache Überleitungsfunktion zwischen den Gliedern der Reihe durch Grundrechenarten? Ich sehe nicht, wie man die kreuzweise Wechselbeziehung als Ausdruck schreiben kann.
4 Antworten

Zur Frage, wie man auf die exakte Formel kommt:
Wir betrachten x und y als Komponenten eines Vektors X.
Dann schreibt sich die Rekursion
Jetzt kommt der Exponenzialansatz
Das führt, wenn man in die Matrixgleichung einsetzt auf
E ist die Einheitsmatrix, M die obige Matrix.
Das liefert die Eigenwerte
mit
Nun zu den Eigenvektoren der Matrix M: diese bestimmen sich zu
Die allgemeine Lösung ist somit
mit den noch zu bestimmenden Konstanten C1, C2: diese ergeben sich aufgrund der Anfangsbedingung
zu
und die berechnete Lösung ist daher nach kurzer Zwischenrechnung
Ich habe dies im Excel mit den Werten der Rekursion verglichen - stimmt exakt:
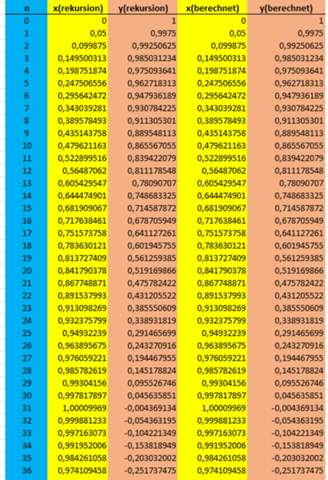
x ist somit ein reiner Sinus mit annähernd Amplitude 1 und y ein Cosinus mit Amplitude 1, wo zusätzlich ein kleiner Sinus überlagert ist. Beide haben annähernd die Frequenz 0.05.
Diese Vorgangsweise ist typisch bei linearen Differenzengleichungen.
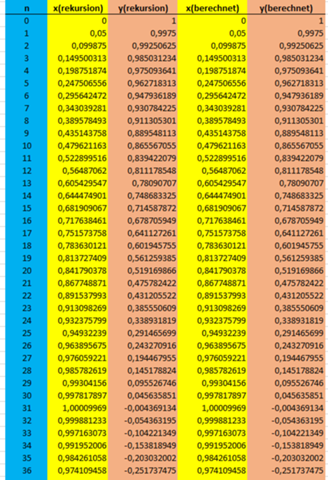

Das scheint wirklich so zu sein, aber beweisen kann ich das auf Anhieb nicht.
Sehr cool, das kannte ich noch nicht!

Ich fange mal mit der typischen Mathematiker-Einleitung an: Das ist eigentlich ganz einfach!
Angenommen, du hast die Komplexe Zahl a + i*b und willst die um einen kleinen Winkel phi drehen. Dann kannst du das schreiben al
(a + i*b) * exp(i*phi).
Jetzt entwickelst du die Exponentialfunktion in einer Talorreihe um phi=0 bis zum linearen Glied:
(a + i*b) * (1 + i*phi) = (a - b*phi) + i*(b + a*phi).
Wenn du jetzt phi durch 0.05 ersetzt und als die Zahl (a + i*b) immer das Ergebnis der letzten kleinen Drehung, erhältst du deine Rekursive Darstellung oben.
Kurz: Ja, das ist eine Approximation von Sinus und Cosinus.

Oh danke! Der Faktor (1 + i*phi) hat mir gefehlt, da ich mich erst in Taylor-Reihen einlesen musste, was das überhaupt ist.
e^ i*phi war mir gerade noch geläufig aus der Elektrotechnik. Der Schritt zu 1+i*phi , war mir verborgen. Hätte auch ohne Taylor drauf kommen können, dass das damit ausmultipliziert zum nächsten Glied führt.
So langsam wird mir klar, was ich da eigentlich für eine Denkhilfe gebastelt habe.

Das ist eine rekursive Differenzengleichung.
mit der Anfangsbedingung
Die Lösung ist (Spalte A) ist (wie man sich durch einen entsprechenden Ansatz überzeugt)
mit
Also ist das weder exakt was Amplitude noch Frequenz betrifft. Du hast nur eine gute Näherung von

es muss natürlich oben heißen
x[n+1] = x[n] + 0.05 y[n]
y[n+1] = y[n] - 0.05 x[n+1]

Ich habe mal per Tabelle Radius und Winkel verglichen. Der Radius bleibt erstmal unter 1, nimmt aber stetig zu und geht langsam auf über 1 bis Ultimo, sodass Du mit der Amplitude >1 wohl recht hast. Hab's aber nicht ganz verstanden, wie Du darauf kommst.
Der Winkel zwischen den Zeilen schwankt doch recht stark, was mehr als nur Rundungsfehler wären. Bei positiven Werten von Spalte A ist die Differenz zur Vorzeile von arctan(B[n]/A[n]) deutlich zu hoch, anderenfalls zu niedrig.
Die Funktion scheint sich etwas zu viel Mühe zu geben, das möglichst schnell auszugleichen. Sorry liebe Funktion für die Vermenschlichung.
Bei Zeile 2 komme ich z.B. auf arctan((1/20)/(399/400)) =arctan(20/399) = 0,05008... (Ich hätte aber damit gerechnet, dass wenigstens der Winkel konstant bleibt.)
und auf r= 0,99875... nach dem Pythagoras.
Was hattest Du für einen Ansatz?
Ich denke aber, mit genügend kleinen Stufen komme ich schnell auf die nahezu exakte Funktion.

Du betrachtest x und y als Komponenten eines Vektors X, schreibst die Rekursion als Matrixgleichung
X[n+1] = M*X[n]
und machst den Ansatz
X = A * exp(i w *n)
Das führt auf eine Eigenwertgleichung, welche dir die Frequenz w liefert.
Es ist praktisch die diskrete Form einer linearen Differenzialgleichung - die Vorgehensweise ist aber exakt gleich.
Ich kann dir das gerne nachher vorrrechnen, hab jetzt aber gleich Unterricht.

Ich habe die detaillierte Rechnung wie man auf die exakte analytische Lösung deiner Rekursion kommt als extra Antwort nochmal formuliert (siehe neue Antwort). Allerdings setzt dies die Kenntnis über Eigenwerte und Eigenvektoren voraus. Diese Theorie kann ich hier nicht wiedergeben, das würde einige Seiten füllen. Zudem kann man dies an tausenden Stellen nachlesen.

Also auf die einleitende Frage ja man kann den Sinus und den Cosinus bzw Approximationen dazu durch die Grundrechnungsarten erhalten.
So verwendet ja zB die Tayloraproximation, oder andere Reihenentwicklungen wie zB Laurent Reihen ja auch nur die Grundrechnungsarten um Funktionen zu approximieren. Auch andere nummerische Algorithmen zB der Cordic Algorithmus verwenden auch nur die Grundrechnungsarten.
Vom Rechenaufwand wirds aber ähnlich sein wie die Taylorapproximation.
Erst einmal ganz großen Dank für die ausführliche Beschreibung. Da geht ja weit mehr, als ich erwartet hätte. Viele einfache Algorithmen ergeben ja ein Labyrinth, was mitunter nicht einmal von Experten gelöst werden kann (Collatz-Problem etc.)
Hier ergibt es einen Sinus in Reinform! Bin echt begeistert.
Mit der obigen Matrix habe ich schon herumexperimentiert, aber muss gestehen, dass ich mit dem Eigenvektor bereits überfordert war, auch wenn ich im Ansatz schon begriffen habe, worauf es hinausläuft. Ist aber ein so spannendes Thema, dass ich mich da unbedingt reinarbeiten will!
Braucht nur seine Zeit, denn ich muss da ein paar Kapitel zurückblättern.