Muss man eine Fallunterscheidung nur bei Beträgen machen?
Meine frage ist wie schon oben erwähnt, ob man eine Fallunterscheidung nur bei Beträgen machen muss. Nehmen wir mal ich habe die Ungleichung 4x^2+3<9, dann wäre x = 1,5. Muss man dann jetzt noch irgendwas machen oder reicht das als Lösung. Wenn ich jetzt aber I x+3 I < 9. Hier muss ich ja eine Fallunterscheidung machen, aber wieso? Ich hoffe ihr könnt mir weiterhelfen. Ihr braucht das auch nicht zu lösen.
7 Antworten

Auch in diesem Fall ist eine Fallunterscheidung insofern erforderlich, als es mehrere Möglichkeiten gibt: die quadratische Gleichung in Linearfaktoren aufspalten, also:
- 4x²=6 → x²=1,5 → x=±sqrt(1,5)....ich bezeichne es weiters als "a"
- (x+a)·(x-a)<0 → es handelt sich also um eine negative Zahl → das Produkt zweier Zahlen kann nur dann negativ sein, wenn eine davon negativ und die andere positiv ist, folglich:
- Fall1: (x+a)<0 und (x-a)>0
- Fall2: (x+a)>0 und (x-a)<0
Anbei eine visuelle Darstellung eines solchen Beispiels mit anderen Zahlen.
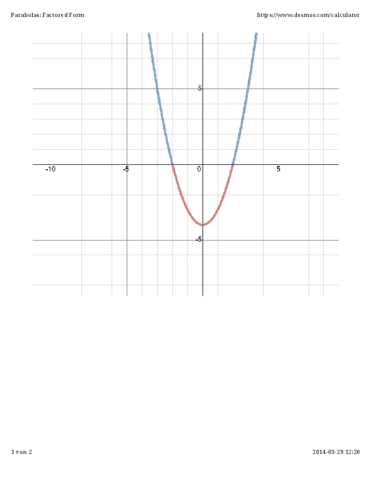

4x²+e<9
erst mal normal umformen
4x²<6
x²< 1,5
und weil es hierfür zwei Lösungen gibt, nämlich
- Wurzel aus 1,5 und - Wurzel aus 1,5
kommt man auf Betrag von x ist kleiner als 1,225. Das heißt ist ist kleiner als 1,225 und gleichzeitig größer als -1,225, liegt also im Bereich zwischen diesen beiden Zahlen. Alle Zahlen aus diesem nach zwei Seiten begrenzten Bereich sind Lösung er Ungleichung.
Bei Ungleichungen, in deren Lösungsverlauf die Quadratwurzel nicht gezogen werden muss, hat man diese Art der Abgrenzung der lösung nach zwei Seiten nicht.

Da Bsp die Wurzel aus vier sowohl - 2 als auch 2 sein kann - du hast also mehrere mögliche Ergebnisse.

kann man das auch rechnerisch ermitteln bevor man diese Fallunterscheidung macht?

die Wurzel ist in der Mathematik positiv definiert. Siehe Wikipedia: Die Quadratwurzel (umgangssprachlich Wurzel; englisch square root, kurz sqrt) einer nichtnegativen Zahl y ist jene (eindeutig bestimmte) nichtnegative Zahl, deren Quadrat gleich der gegebenen Zahl y ist. Au, was haben wir mit unserem Mathelehrer darüber gestritten. Beim Studium haben wir es dann eingesehen.
Die Lösungen x der Gleichung x^2=b sind x1=+Wurzel(b) und x2=-Wurzel(b).

Das glaube ich so gerne, jedoch wurde mir in zahlreichen LK Klausuren ein Fehler angestrichen, als ich nur den nichtnegativen Wert genannt habe --> vielleicht sollte das mal meiner Lehrkraft vorhalten, vielen Dank! :D

dass man beim Betrag ne Fallunterscheidung machen muss, liegt an der Definition des Betrages; Ix+3I = x+3 , wenn x+3>0
und Ix+3I = -(x+3) , wenn x+3<0
da man x nicht kennt, muss man die Fallu. machen.

ich weiß nicht, wie du bei 4x^2+3<9 auf 1,5 gekommen bist denn 4*1,5^2=9. Löse bitte mal die Gleichung 4x^2+3=9. Du bekommst dann erstmal x^2=(9-3)/4=1.5. Und es gibt zwei Lösungen x1 = -Wurzel(1,5) und x2 = +Wurzel(1,5). Die Ungleichung ist also erfüllt wenn x zwischen x1 und x2 liegt, d.h. |x| < Wurzel(1,5) ist. Wenn du das verstanden hast, ist dir der Rest deiner Frage sicherlich klar.

achso, ja ich habe vergessen die Wurzel zu ziehen. Also ist L=-Wurzel(1,5)<x<Wurzel(1,5). Schreibt man das so?