Könntet ihr mir bei der speziellen Relativitätstheorie helfen?
Hallo,
Ich besuche derzeit die 10. Klasse weswegen ich bezweifele das ich einen großen Durchbruch im Bereich der Widerlegung der speziellen Relativitätstheorie erreicht habe. Aber als ich versuchte die spezielle Relativitätstheorie in Form der Formel m= m0 geteilt durch die Wurzel aus 1 minus v zum Quadrat durch c zum Quadrat (entschuldigt, ich weiß nicht wie man Mathematische Zeichen wie Wurzeln und Bruchstriche auf dem Handy schreibt) auf Photonen zu übertragen ist mir folgendes aufgefallen:
Der oben genannte und unten zum Verständnis abfotografierte Formel können konkrete Zahlen eingesetzt werden. Hierzu verwende ich folgendes:
Rohmasse eines Photons : 0
Geschwindigkeit eines Photons : v
Ich komme also ausgerechnet auf folgendes :
M = 0 / Wurzel 1 v Quadrat geteilt durch v Quadrat.
<=> m= 0/ Wurzel 1-1
<=> m= 0/ Wurzel 0
<=> m= 0/0
Dies stellt mich vor folgende Fragen:
1. 0/0 ist nicht definiert, hat ein Photon also eine nicht definierte Masse?
2. alleine durch die Bewegung müsste es doch eine Bewegungsenergie und somit Masse besitzen (oder? Ist bei Strings doch ähnlich da sie ja ebenfalls Rohmasse Null haben und die Masse durch Energie gewinnen ?) was man durch die Formel e= m * c zum Quadrat nachweisen kann. Müsste man sich also dem Punkt Null durch null annähern ? Dann käme man auf + oder - unendlich, da ich eine Negative Masse für Photonen ausschließe wäre nur +unendlich möglich. Ein Photon kann aber doch schlecht unendlich Masse besitzen oder ?
Ich würde mich über konstruktive Antworten sehr freuen und Danke bereits im Voraus,
LG Jascha
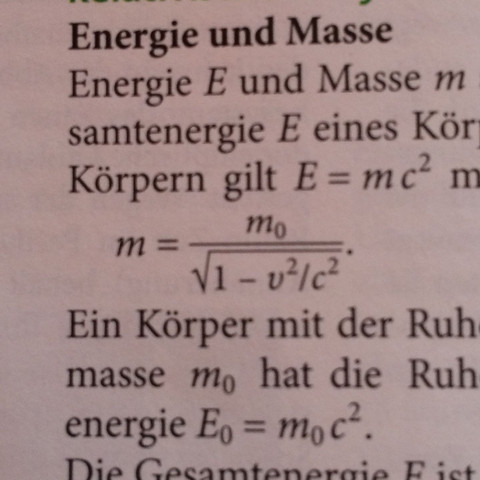
6 Antworten

Also ein Proton hat eine Masse von 0. ob das mit nicht definiert gleichzusetzen ist weiß ich auch nicht. Ich kann mir aber vorstellen das jene Formel von Einstein einzig für massebehaftete Objekte gilt.
Was die Energie angeht: Formel der kinetischen Energie in der klassischen Physik lautet: 1/2*m*v^2.
m ist 0 somit die kinetische Energie auch. Was es aber mit der elektrischen Energie die das Photon ja als übertraugungsteilchen der Elektromagnetischen Wrchselwirkug auf sich hat weiß ich auch nicht. Leider.

Also ein Proton hat eine Masse von 0. ob das mit nicht definiert gleichzusetzen ist weiß ich auch nicht.
Du meinst Photon. Das Proton hat sogar ziemlich viel Masse.
Ich kann mir aber vorstellen das jene Formel von Einstein einzig für massebehaftete Objekte gilt.
Natürlich. Masselose "Teilchen" (ein Photon ist eigentlich kein Teilchen, sondern eine Energieportion, aber das ist eine andere Geschichte) bewegen sich mit c, und da ist
γ = 1/√{1–β²}, β=v/c
natürlich nicht definiert und die Formel nicht anwendbar.
Was die Energie angeht: Formel der kinetischen Energie in der klassischen Physik lautet: 1/2*m*v^2. m ist 0 somit die kinetische Energie auch.
Nein. Die Aussage ist zwar folgerichtig, aber die klassische Formel ist natürlich überhaupt nicht für Geschwindigkeiten anwendbar, bei denen man die Impulsmasse Eₖ/c² der kinetischen Energie berücksichtigen muss.
Schon wenn man Eₖ₀=m·v²/2 ansetzt, was mathematisch nicht ganz sauber ist, so hat diese Energie die Impulsmasse m·v²/2c² und damit die Energie Eₖ₁=m·v²/2c²(v²/2), die dazu addiert werden muss, usw. ...
Es entsteht eine geometrische Reihe in v²/2c², die gegen
mc²(1/(1–v²/2c²)–1)
konvergiert, was nicht ganz der korrekten Formel
mc²(γ–1) = mc²(1/√{1–(v/c)²} – 1)
entspricht. Doch auch diese Formel hat die klassische Formel als v≪c - Näherung.
Andererseits wird für v→c γ≫1, d.h. bei sehr schnellen Teilchen kann man mc²=E₀ gegen E bzw. Eₖ=E–E₀ vernachlässigen. Bei Photonen ist γ nicht mehr definiert, aber man kann sagen, dass sie gleichsam komplett aus ihrer kinetischen Energie bestehen.

ein photon hat die masse m=0 und die geschwindigkeit v=c. in jedem bezugssystem.
die korrekte formel, die den zusammenhang zwischen impuls p, masse m und energie E herstellt lautet.
E²=m²*c^4 + p²c²
da für photonen gilt m=0, vereinfacht sich dies zu E=pc
der zusammenhang zwischen energie E, masse m und geschwindigkeit v lautet.
v=c * Wurzel[1 - (mc²/E)²]
daran erkennst du, dass für teilchen mit m>0 immer gilt v<c, ganz egal wie sehr du die energie auch erhöhst. andererseits gilt für teilchen ohne masse, also m=0 (wie z.B. photonen), v = c. ganz unabhängig von der energie und damit vom bezugssystem.
PS: ich weiß, ich weiß dass man auch heute noch überall den mist von der "relativistische masse" und E=mc² auch für bewegte teilchen und so weiter lesen kann. aber glaube mir: vergiss das einfach. auch wenn es in allen populärwissenschaftlichen büchern steht und auch lehrer das heute, nach über hundert jahren, immer noch unterrichten: es ist unsinn, und wird in der physik so seit bald hundert jahren nicht mehr verwendet.

Ist gut beobachtet.
Daher sagt man ja auch, dass das Photon keine Ruhemasse hat. Durch seine Bewegung hat es aber Energie (und die kann man natürlich auf eine Masse umrechnen, das ist aber keine Ruhemasse).
Ich hätte mal gesagt, die Formel ist nur bei m0>0 anwendbar (also bei "echten" Teilchen, die auch eine Ruhemasse haben, wie Protonen und so). Bei einem Photon wird wegen v=c der Nenner 0, und so ein Bruch ist natürlich nicht definiert.
Stehen da noch Randbedingungen?


Ich meine: steht da noch, wann man die Formel anwenden darf (und ggf. wann nicht)?

Also in dem mir vorliegenden Buch gibt es leider keine Randbedingungen für die Formel (solltest du diese meinen) aber ich könnte mir gut vorstellen die Formel nur für m<0 gilt, was dann vermutlich erst in höheren Schulbüchern erwähnt wird.

Ok. Ich habe nur was von "Körpern" gelesen, ich könnte mir vorstellen, dass ein Photon nicht unter diese Definition von Körper fällt. Ist aber nur so eine Idee.

Es gibt einen Eintrag von 2014 "Relativitätstheorie und Gewicht von Photonen.", da schreibt auch jemand, dass die Formel für Photonen nicht anwendbar sei (da Ruhemasse nicht existent ist).

Ich besuche derzeit die 10. Klasse weswegen ich bezweifele das ich einen
großen Durchbruch im Bereich der Widerlegung der speziellen
Relativitätstheorie erreicht habe.
Ob Du einen Durchbruch in der Widerlegung der SRT erreicht hast oder nicht, hängt erst mal nicht davon ab, ob Du Schüler oder Professor bist.
Selbsternannte Einsteinwiderleger sind nicht selten Professoren, was sie nicht daran hindert, bei ihren "Widerlegungen" eine erschreckende Ahnungslosigkeit in Sachen klassischer Physik zu offenbaren, weshalb ich diese Leute gern auch Newtonversager nenne. Ich habe allerdings den Verdacht, dass es aber häufig gar keine Unwissenheit mehr ist, sondern eine bewusste Verbiegung der Newtonschen Physik, um die eigenen Argumente zu retten. Schließlich wollen sie die SRT nicht nur als falsch, sondern als von vornherein ganz und gar unsinnig darstellen, wie sich einst Stalin nicht damit begnügte, seine potentiellen Opfer einfach umbringen zu lassen, sondern sie auch gesellschaftlich vernichten wollte, deshalb die Schauprozesse. Deshalb betreiben sie Rabulistik und zünden Nebelkerzen.
Deine Überlegung hingegen ist eine grundsolide. Dass sie die SRT widerlegt, ist dagegen auch aus Deiner Sicht sehr unwahrscheinlich, denn sie ist zu einfach, um nicht schon lange zur Widerlegung der Theorie durch Mathematiker geführt zu haben. Insofern ist Deine Anfangsüberlegung (s. Zitat) durchaus stichhaltig.
Allerdings darf man Größen, die 0 werden oder sein können, nicht mit dem Vorschlaghammer bearbeiten, indem man einfach dividiert, denn dadurch erzeugt man Widersprüche, weil die 0 der große "Plattmacher" im Reich der Zahlen ist
0·z = 0 ∀ z ∈ ℂ
(∀ heißt "für alle", ℂ ist die Menge der Komplexen Zahlen; sie ist besonders umfassend und enthält insbesondere ℝ) und daher keinen und insbesondere keinen eindeutig bestimmten Kehrwert hat, auch nicht etwa ∞. Durch 0 dividieren ist somit unmöglich, da Division sich als Multiplikation mit dem Kehrwert auffassen lässt (wenn dieser in der betrachteten Zahlenmenge, etwa in ℤ, der Menge der Ganzen Zahlen, nicht enthalten ist, dann zumindest in einer Einbettung in eine Obermenge).
Das Problem stellt sich aber nicht erst bei der SRT, sondern schon bei relativ einfachen Problemen wie der Momentangeschwindigkeit in zum Zeitpunkt t₀ in 1D, etwa in x-Richtung. Dort ist
v︦ₓ([t₀, t₀+∆t]) = {x(t₀+∆t) – x(t₀)} / {(t₀+∆t)–t₀}
die Durchschnittsgeschwindigkeit eines Körpers im Zeitintervall [t₀, t₀+∆t]. Die Momentangeschwindigkeit vₓ(t₀) kann selbstverständlich nicht einfach ∆t=0 gesetzt werden, denn dann käme dasselbe "0/0" heraus wie bei Deiner Überlegung. Man muss eine Grenzwertbetrachtung anstellen:
vₓ(t₀) = lim_{∆t→0}{ v︦ₓ([t₀, t₀+∆t]) } ≕ ẋ(t₀) oder dx/dt (t=t₀)).
Dabei heißt ẋ(t₀) respektive dx/dt (t=t₀) die Ableitung von x nach t an der Stelle t=t₀, wobei Physiker das meistens nicht so eng sehen mit den genauen Definitionen; ihnen genügt, dass dt "so klein ist, dass man es als unendlich klein idealisieren kann" und behandeln es wie einen normalen Nenner. Entscheidend ist, dass sich der Quotient nicht mehr ändert, wenn man dt noch kleiner macht.
So kann man auch mit der Ruhe- oder besser Eigenmasse µ=E_ph/c² des Photons verfahren: Man nimmt an, sie sei nicht exakt 0, sondern nur "unendlich" klein und betrachtet dann, was geschieht, wenn dieses Teilchen mit einer "unendlich" nahe bei c liegenden Geschwindigkeit bewegt. Dabei ist die kinetische Energie oder auch die Gesamtenergie (kinetische Energie + (vernachlässigbarer) Ruheenergie µc²) konstant zu halten.
Wenn man es mathematisch sauber haben will, kann man auch die Nichtstandard-Analysis anwenden. Sie enthält zur Absicherung ihrer Definitionen und Axiome eine ganze Menge hartes Holz, aber dann wird alles plötzlich ganz einfach, weil man auf einmal aktual-unendliche Größen (also solche, die nicht gegen Unendlich oder gegen 0 streben, sondern unendlich groß oder unendlich klein sind, ohne gleich 0 zu sein) wie gewöhnliche Zahlen beschreiben kann. Im Rahmen der Nichtstandard-Analysis könnte man dem Photon eine infinitesimale Eigenmasse zuschreiben, die nicht gleich 0 ist.

@jaschaweber: Du hast mir eine Frage gestellt, und ich kann diese nur hier beantworten:
Aber noch eine Frage: wenn ich mit Grenzwerten hantieren müsste würde dies doch bedeuten dass es unmöglich ist die gesamte Masse unter Einbezug der kinetischen Energie eines Photons zu berechnen oder?
Nein, warum?

Im Vorfeld der Grenzwertbetrachtung muss ich dringend noch einen (wohl müdigkeitsbedingten) Fehler korrigieren, denn
So kann man auch mit der Ruhe- oder besser Eigenmasse µ=E_ph/c² des Photons verfahren
ist falsch: E_{ph}/c² ist sozusagen die effektive oder dynamische Masse des Photons und gerade nicht seine Eigenmasse. Die ist 0.
Soll µ die Eigenmasse eines Teilchens der Energie E sein, das sich mit
v = c(1 – δ) mit δ≪1
bewegt, dann ist sie
µ = E/γc² = E(√{1 – (v/c)²})/c²
= E(√{1 – 1 + 2δ – δ²)})/c² ≈ E√{2δ}/c²,
denn δ² kann man bei kleinem δ erst recht vernachlässigen.

Melde ich mich nochmal^^:
https://www.uni-ulm.de/fileadmin/website_uni_ulm/nawi.inst.251/Didactics/quantenchemie/html/PhImpF.html
Das erklärt schon einiges.
Da die Ruhemasse des Photons 0 ist fällt m0 einfach weg womit sich m=0 ergibt. :)

Ich verstehe nicht so ganz wieso m0 wegfällt.... Die Formel auf der Website beschreibt doch lediglich das Verhältnis zwischen Masse und Rohmasse, das Photonen keine Rohmasse haben ist klar, wie auf der Website ja ziemlich schlüssig erklärt. Doch wieso fällt m0 weg da es null ergibt? Ich muss ja die Rohmasse durch etwas teilen und nicht addieren oder subtrahieren. Null ist also nicht das neutrale Element, wieso fällt sie weg?
Tschuldige sollte die Frage blöd sein da ich irgendeinen deutlichen Zusammenhang nicht sehe,
LG Jascha

Einfacher vielleicht so:
Du formst die Formel um so dass der Nenner nach oben kommt. Um das zu erreichen nimmst du ihn hoch -1.
also steht da M0* Wurzel aus ... Hoch -1.
somit stellt die 0 kein Problem da und es ergibt 0.
Wäre als würde man 0 einfach gleich wecklassen würd ich mal sagen:)
Hoffe ich hab das jetzt richtig^^
Danke für die Information! Natürlich meinte ich Photon. Warum auch immer ich hier Proton geschrieben hab ist mir ein Rätsel...