Was ist die aktuell höchste berechnete Fibonacci Zahl (mit index) und wo finde ich diese Art von Rekorden?
7 Antworten

Da diese ganzen Zahlen recht einfach zu berechnen sind (im Gegensatz zu echten Primzahlen {nicht die "nextprobableprime"}) und ganze Zahlen im Gegensatz zu irrationalen Zahlen kaum interessante Ziffernverteilungen haben, werden sie selten gelistet.
Mein PC rechnet Fibonacci(100000000) ohne Optimierung (nur 1 Kern und Interpreter statt Compiler; keine AVX-Befehle) in etwa 6 min aus.
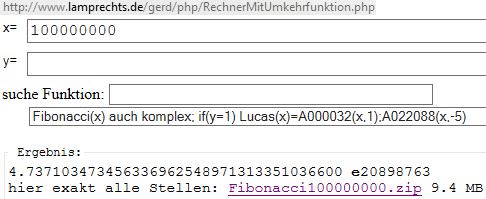
Bei http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
- kann man bis Fibonacci(2003) alle Stellen sehen
- danach wie die meisten Rechner in Exponentialschreibweise
- einige wie Fibonacci(100000000) kann man downloaden (siehe Bild)
Hier noch ein Beispiel um zu zeigen, wie leicht man
Fibonacci(500000000) berechnen kann:
5.963543132432416200383748... e104493819
die letzten Stellen lauten: ...9453125
zu: "...wo Rekorde...?"
http://www.numberworld.org/y-cruncher/records.html
Größtes Problem ist nicht die Berechnung, sondern:
- PC finden, der mehrere Tage stabil läuft
- Festplatten-Lebensdauer erfordert RAID-System, bei dem man HD's im laufenden Betrieb tauschen kann und Zwischen-STOP, ohne völlig neu starten zu müssen
Die Physik bremst uns aus!
Die 13.3 TB von Pi haben fast 1 Jahr gebraucht und die 20 TB ist mit der Lebensdauer von "normalen" Bauelementen kaum realisierbar.

Interessantes zu Fibonacci(100000000):
obwohl es keine irrationale Zahl ist, zeigt die Ziffernverteilung pro 5 Mio Stellen eine gute Gleichverteilung:
1. 5 Mio.:
Ziffer | absolut | rel. %
0 500779 10.015580000000001
1 499720 9.9944
2 499148 9.98296
3 500680 10.0136
4 500331 10.006620000000001
5 499491 9.989820000000001
6 499701 9.99402
7 499358 9.987160000000001
8 499987 9.999740000000001
9 500805 10.016100000000001
2. 5 Mio:
0 501230 10.024600000000001
1 499215 9.984300000000001
2 498337 9.966740000000001
3 500835 10.0167
4 500798 10.015960000000001
5 500167 10.003340000000001
6 500588 10.01176
7 499603 9.99206
8 499182 9.983640000000001
9 500045 10.000900000000001
...
Rest:
1 89674 9.977480183896995
2 90056 10.019982998874008
3 89806 9.992167020485911
4 89461 9.953780970310337
5 89971 10.010525566222055
6 90269 10.043682212460668
7 90324 10.049801727706048
8 89867 9.998954119212607
9 89739 9.984712338277901

Habe gerade Fibonacci(1 Mrd.) exakt ausgerechnet -> bin ich nun Weltmeister?

Hallo,
allgemein gesehen sind und streben Zahlen ins unendliche. Du wirst immer eine größere Zahl und eine kleinere Zahl finden.
Rekorde sind theoretisch gesehen garnicht vorhanden, da wie gesagt die Zahlen ins unendliche streben, das ist allerdings eine abstrakte Meinung, muss man nicht verstehen :)
Viele Grüße,
Siedler

Die Fibonacci Zahlen sind sehr leicht zu bestimmen. Wenn man zwei aufeinanderfolgende Zahlen kennt, kann man die nächste einfach durch die Summe der beiden Zahlen ausrechnen.
Außerdem gibt es sogar eine (relativ einfache) geschlossene Formel für die n-te Fibonacci-Zahl, die du auch leicht auf Wikipedia nachlesen kannst. Da muss man nur die Zahl n einsetzen und bekommt quasi sofort ohne großen Rechenaufwand die n-te Fibonacci-Zahl heraus.

Die geschlossene Form der Fibonacci-Folge enthält allerdings irrationale Faktoren. Dadurch erhält man immer Fehler in der Rechnung. Außerdem muss man für große n sehr große Potenzen berechnen und je nach Prozessor ist ein jeweils anderer Mix aus Additionen und Multiplikationen notwendig, um das Rechenwerk möglichst effizient zu nutzen.
Insofern ist es nicht so trivial wie man denkt bei vorgegebener Rechenzeit und Rechenleistung die größtmögliche Fibonacci-Zahl zu berechnen, auch wenn es zugegebenermaßen deutlich unspektakulärer als z.B. bei Primzahlen ist.

Es gibt eine aktuell höchste Primzahl, doch Fibonacci Zahlen sind viel zu einfach zu berechnen, um eine höchste zu haben. Sobald eine errechnet wurde, kann man sofort die nächste bestimmen.

Meinst du vielleicht Primzahlen? Da wären wir grade bei 2^74.207.281-1 mit etwas über 22 Millionen Ziffern.