Was bedeutet: Das Dreieck ABC isy gleichschenklig mit der Basis [BC] Und wie zeichne ich das?
Hi ich schreib morgen eine Mathe ex und weiß nicht wie man das zeichnen soll. Was ist eine Basis und wie zeichnet man das? Lg
4 Antworten

Gleichschenklig bedeutet, dass 2 der 3 Seiten des Dreiecks gleich lang sind.
Die Basis ist in diesem Bsp die Strecke BC = auf ihr "stehen" die beiden gleich langen Schenkel.
Wie man es zeichnen kann, hängt von den vorgegebenen Werten ab.
Ich habe dir ein Bsp in den Anhang gesetzt.....
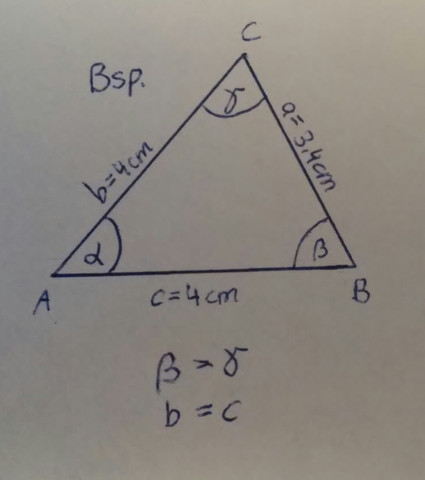

Vielen lieben Dank für deine Mühe ich hab es nun verstanden:)

Mit der Basis ist die Grundseite des Dreiecks gemeint, welches in deinem Fall die Strecke zwischen dem Punkt Bund C darstellt. Bei einem gleischschenklichen Dreieck sind 2 Seiten genau gleich lang. In deinem Fall also die Strecken AB und AC. Die Winkel zwischen den Strecken AB und Basis, sowie AC und Basis sind somit ebenfalls gleich groß.


Die Basis eines gleichschenkligen Dreiecks ist die Seite, auf der die beiden gleichen Winkel und die beiden Schenkel liegen.
Wenn das Dreieck ABC also gleichschenklig mit der Basis [BC] ist, so heißt das nichts anderes, als dass die beiden gleichen Winkel ABC und BCA sind.
Wenn du ein solches Dreieck zeichnen sollst, so zeichnest du einfach die Seite BC, konstruierst ein Lot (eine Senkrechte) auf BC und verbindest die beiden Ecken mit dem Lot.
Ich hoffe, ich konnte dir helfen; wenn du noch Fragen hast, kommentiere einfach.
LG Willibergi


kann ich mir nur so vorstellen: B-C sind z.B. 20 cm; dann sind B-A und C-A auch jeweils 20 cm.
... das wäre ja gleichseitig