Ich habe mal eine Frage: wie kam Newton zur m/r zum quadrat abhängigkeit der Gravitationskraft znd wie konnte er sein Ergebnis prüfen?
3 Antworten

Interessanterweise kann man zwei Dinge zeigen: Wenn ein Gravitationsgesetz auch nur eine kleine Abweichung von 1/r^2 zeigt, also zum Beispiel 1/r^(2,02), dann gibt es keine geschlossenen Bahnen der Planeten mehr, das 1/r^2 ist also Voraussetzung. Außerdem folgt aus dem Feldbegriff (den Newton aber noch nicht hatte) und unserer dreidimensionalen Welt, dass man ein 1/r^2 Gesetz hat. Wenn die Feldlinien nämlich von einem Punkt radial nach außen weggehen, dann durchstreifen sie in doppeltem Abstand die vierfache Fläche. Wären wir zum Beispiel in einer zweidimensionalen Welt, dann gingen die Feldlinien so auseinander, dass in doppeltem Abstand auch die durchströmte Linie (ist dann keine Fläche mehr) doppelt so groß ist, in einer zweidimensionalen Welt hätten wir also ein 1/r Gravitationsgesetz, und nach dem zuerst Gesagten ist dann klar, dass es dort keine geschlossenen Planetenbahnen gibt.
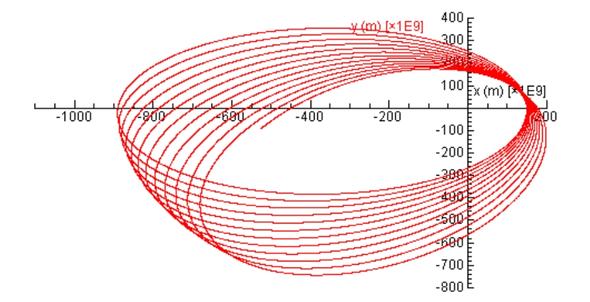

Im Bild ist eine Planetenbahn mit einem 1/r^(2,02) Gesetz zu sehen, habe ich mit einem Modellbildungssystem modelliert.

Newton kannte das 3. Keplersche Gesetz: (T1 : T2)² = (a1 : a2)³. T ist die Umlaufzeit und a ist die große Halbachse des Planeten. Bei einer Kreisbahn ist a gleich dem Radius r. Die Zentralbeschleunigung a nimmt mit dem Quadrat des Abstandes ab: a = c/r² ( c ist eine Konstante). Mit a = w² * r (w ist die Winkelgeschwindigkeit Omega) erhält man w²r = c/r² und w² = c/r³. Wegen w = 2 pi / T ist (2 pi / T)² = c/r² und 4 pi / T² = c / r³ Also ist T² proportional zu r³. Da die Zentralbeschleunigung proportional zur Gravitationskraft ist, nimmt die Anziehungskraft der Sonne mit dem Quadrat des Abstandes ab.

Die Gravitations-/Schwerkraft nimmt eben (überprüfbar mit Erdbeschleunigung) nach aussen hin nicht linear ab, sondern eben potentiell!