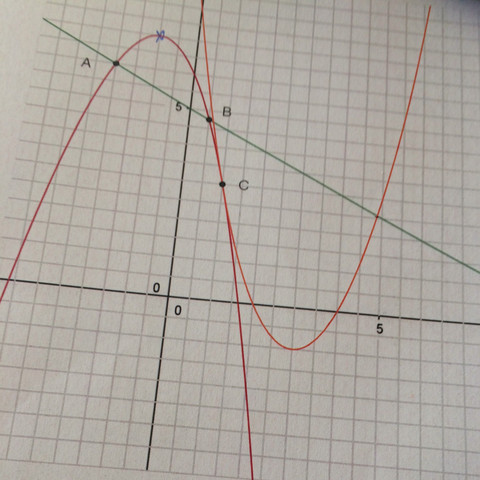
"Die beiden Parabel berühren sich im Punkt C. Zeigen Sie dies durch Rechnung?
Die Linke Parbel hat die Parabeln Gleichung y= -1/2x + 5
Die Parabel p2 hat denn Schnittpunkt (3/-1)
Man soll die Gleichung dazu ausrechnen . Das habe ich gemacht und raus ist, y=x^2 - 6x - 1
Jetzt soll man die beiden gleichsetzen und es ausrechnen mit der pq-formel aber bei mir kommt kein Ergebnis raus.
Kann mir jemand helfen?
5 Antworten

y=-1/2x+5 ist die Gleichung der eingezeichneten Geraden!
Die Parabeln sind beides Normalparabeln; siehst Du daran, dass vom Scheitelpunkt S(x_s|y_s) aus gesehen, bei x_s+1 der y-Wert um eins höher bzw. niedriger liegt;
aufgrund des Scheitelpunktes kannst Du jetzt die entsprechende Funktionsgleichung der linken Parabel ermitteln: f(x)=-(x+1)²+7=-x²-2x+6
von der rechten Parabel ist der Schnittpunkt bekannt, somit hast Du als Gleichung erst einmal: g(x)=a(x-3)²-1
um das a zu ermitteln, rechnest Du f'(1)=g'(1), da im Berührpunkt C beide Steigungen gleich sind und löst nach a auf.

Und (3/-1) ist der Scheitelpunkt, nicht der Schnittpunkt.

Bei der pq-Formel ist wichtig dass das x^2 alleine steht... Also da darf nicht sowas wie 3,5x^2 stehen. Vielleicht hilft das.

die parabel hat die form y= (x-3)^2 -1 = x^2 - 6x + 8

die parabel hat die gleichung y=-(x-2)^2 +7


